Příklad: Rozviňte danou funkci v mocninnou (Taylorovu) řadu s daným středem.

Řešení: Použijeme standardní postup. Která funkce bude základem pro náš rozklad? Není tam exponenciála, sinus ani kosinus, takže vylučovací metodou to bude buď geometrický rozvoj nebo nějaký pokročilejší trik. Můžeme z toho udělat něco, co vypadá (přibližně) jako funkce 1/(1 − y)? Vidíme, že hlavním problémem je to x v čitateli, ale toho se snadno zbavíme pomocí dělení se zbytkem. Tak tedy začneme, pak přejdeme na první krok, změníme všechna x tak, aby místo nich byly výrazy (x − 1).

Teď budeme následovat standardní postup k vytvoření 1 − y ve jmenovateli. Nejprve změníme "2" na "vedoucí 1", pak upravíme znaménko za ní.

Teď už jsme připraveni rozvinout tuto funkci pomocí geometrické řady, zde je třeba opatrnosti ohledně platnosti rozvoje. Pak řadu přeorganizujeme tak, aby se v ní objevily výrazy (x − 1). Také použijeme distributivní zákon a přesuneme výrazy, které jsou před řadou, dovnitř.

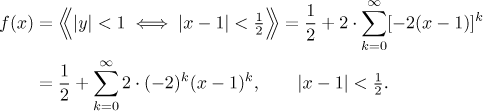
Poznamenejme, že ten zlomek 1/2 je vlastně také řada, jmenovitě řada, jejíž člen a₀ je 1/2 a všechny ostatní členy jsou 0, a tyto dvě řady se překrývají, protože také druhá řada obsahuje absolutní člen. Abychom vytvořili jen jednu řadu, tak rozdělíme tu druhou na dvě části, absolutní člen a zbytek, a pak dáme absolutní členy dohromady. Nejprve ovšem hlavní řadu mírně změníme, aby vypadala lépe.

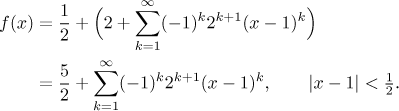
Bonus: Daná funkce je vlastně podíl dvou funkcí, které umíme rozvinout v mocninnou řadu, můžeme proto zkusit tento podíl rozvinout pomocí metody neurčitých koeficientů. Napíšeme čitatel a jmenovatel jako řady, což je docela snadné. Jsou to polynomy, tudíž je prostě přepíšeme tak, aby se tam vyskytovaly členy (x − 1). Výsledný podíl je "pěkný" v 1 (nedělíme nulou při x = 1), proto jej lze také rozvinout v mocninnou řadu, napíšeme to jako obecnou řadu s koeficienty a_k.

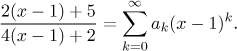
Teď obě strany vynásobíme jmenovatelem, abychom se zbavili zlomku, a pak přepíšeme vzniklé řady napravo jako jednu řadu. Naštěstí na to nebudeme potřebovat použít Cauchyho součin, protože jedna z těch dvou řad je "konečná", má jen konečně mnoho nenulových členů.

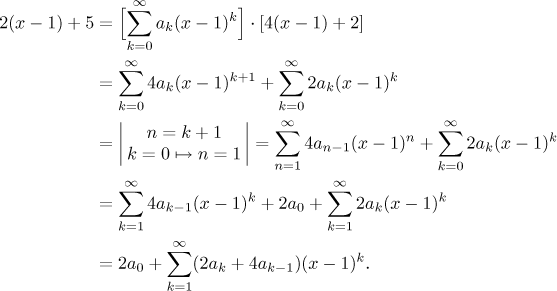
Na třetím řádku jsme v první řadě posunuli index, abychom měli správnou mocninu, pak jsme museli oddělit první člen druhé řady, aby měly ty dvě řady napravo stejné indexování.

Získali jsme rovnost dvou řad, takže podle jednoznačnosti rozvoje se musí odpovídající koeficienty nalevo a napravo rovnat.

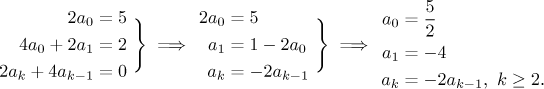
Když ten poslední vzorec použijeme rekurzivně, dostaneme a₂ = 8, a₃ = −16, a₄ = 32, můžeme také odhadnout a pak dokázat indukcí, že vlastně a_k = (−1)^k2^k+1. Toto formálně platí pro všechna k > 1, ale i koeficient a₁ do tohoto vzorce zapadá. Nakonec tedy získáme stejnou řadu jako předtím.

Další příklad
Zpět na Řešené příklady - Řady funkcí