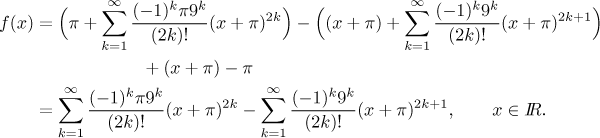Příklad: Rozviňte danou funkci v mocninnou (Taylorovu) řadu s daným středem.
![]()
Řešení: Použijeme standardní postup. Vidíme, že když rozvineme ten kosinus, tak je to hlavní za námi, zbytek už se udělá snadno. Daná funkce tedy už má rozumný tvar a můžeme přejít k prvnímu kroku, změníme všechna x tak, aby se místo nich objevily výrazy
Tady to je:
![]()
Kdybychom teď rozvinuli kosinus, tak by měla výsledná řada členy jako v
jeho argumentu a nebyla by mocninnou řadou se středem
![]()
Teď už jsme připraveni rozvinout kosinus pomocí řady pro
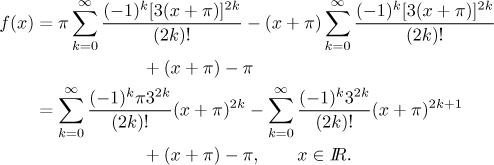
Všimněte si, že rozvoj kosinu platí pro všechna
Výsledek je vyjádřen jako součet dvou mocninných řad, ale čeká se, že to bude jen jedna řada. V posledním kroku tedy obvykle spojíme obě řady do jedné. V tomto případě by to ale bylo dosti nepříjemné, protože jedna řada obsahuje pouze liché mocniny a druhá pouze sudé, takže se nepřekrývají. Kdybychom opravdu chtěli vytvořit jen jednu řadu, tak bychom do ní museli dát obecné koeficienty ak a pak popsat jejich hodnoty podle toho, zda je k sudé či liché, takže bychom to čtenáři rozhodně neulehčili, možná by to bylo i horší. V případě nepřekrývajících se řad je tedy tradičně necháváme, jak jsou.
Zde by se vlastně jedna věc udělat dala, každá řada má jeden člen společný s
tou konečnou řadou vedle, jmenovitě se mocnina