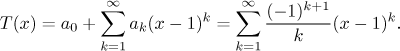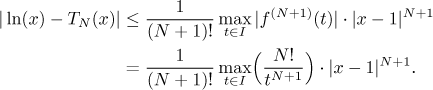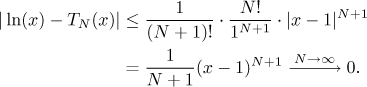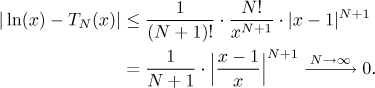Taylorova řada pro logaritmus

Nejprve odvodíme Taylorovu řadu pro f (x) = ln(x) se středem a = 1.
Je snadné indukcí dokázat, že pro všechna přirozená čísla k je k-tá derivace rovna f ^(k)(x) = (−1)^k+1(k − 1)!/x^k, tudíž koeficienty jsou

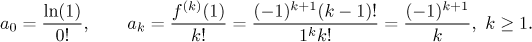
Museli jsme (a budeme muset) pracovat s případem k = 0 zvlášť, protože f ⁽⁰⁾ = f nezapadá do toho obecného mustru. Taylorova řada je

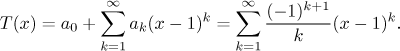
Teď zvolme libovolné číslo x z intervalu (0,2). Použijeme Lagrangeův odhad zbytku k důkazu, že tato Taylorova řada konverguje k logaritmu v tomto x. Když označíme jako I uzavřený interval s krajními body 1 a x, dostaneme odhad

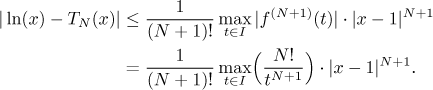
Teď potřebujeme vědět, kde je x. Jestliže x = 1, pak T(1) = 1 = ln(1). Jestliže x > 1, pak je interval I roven ⟨1,x⟩, a protože 1/t^N+1 je klesající funkce, maximum nastane v 1. Proto

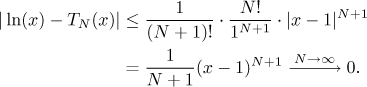
Použili jsme fakt, že x < 2, proto (x − 1) < 1 a víme, že q^N jde k nule pro |q| < 1 (viz geometrická posloupnost). Takže pro x > 1 (a samozřejmě x < 2) máme konvergenci T(x) k ln(x) dokázánu.

Když x < 1, pak je interval I roven ⟨x,1⟩ a maximum klesající funkce 1/t^N+1 se nabývá v x. Proto

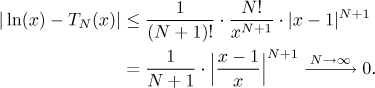
Teď máme malý problém. Jestliže x > 1/2, pak je to číslo v absolutní hodnotě menší než 1 a dostaneme konvergenci díky staré dobré geometrické posloupnosti. Na druhou stranu, pro x mezi 0 a 1/2 tento argument selhává, protože číslo v geometrické posloupnosti je větší než 1 a horní Lagrangeův odhad tedy jde do nekonečna. Všimněte si ale, že to je pouze horní odhad, takže to nemusí nutně znamenat, že i rozdíl |ln(x) − T_N| jde do nekonečna. A také nejde, my víme, že ve skutečnosti i tam k nule jde, protože v sekci Teorie - Řady funkcí - Taylorova řada jsme dokázali pomocí jiné metody, že ona Taylorova řada konverguje logaritmu na (0,2⟩. To ukazuje, že na (0,1/2) je Lagrangeův odhad příliš marnotratný.