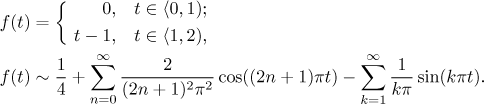
Našli jsme následující Fourierovu řadu (pro periodické rozšíření):
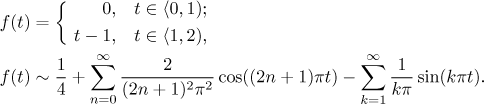
Trigonometrické polynomy prvních pěti stupňů jsou
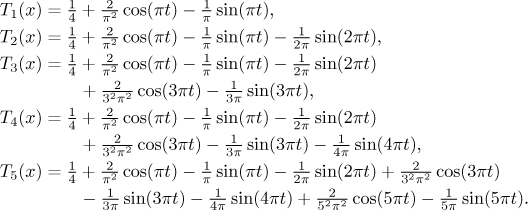
Teď je nakreslíme, abychom viděli, jak se částečné součty přizpůsobují periodickému rozšíření dané funkce.
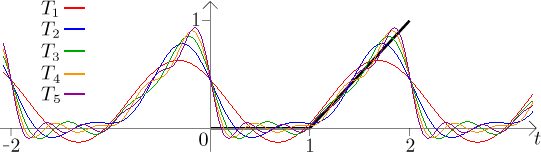
Abychom viděli, jak to vypadá s delšími částečnými součty, soustředíme se
teď na základní periodu, tedy na interval
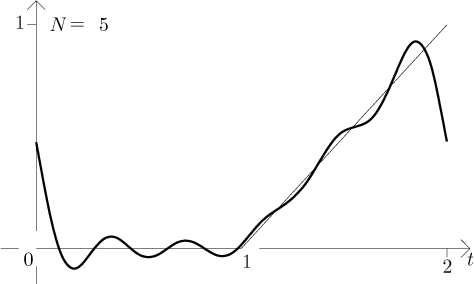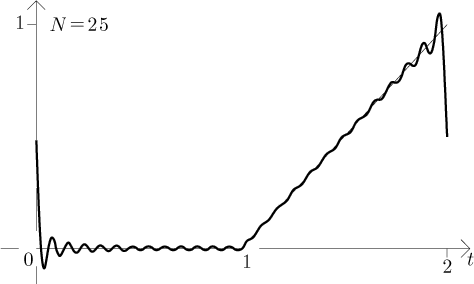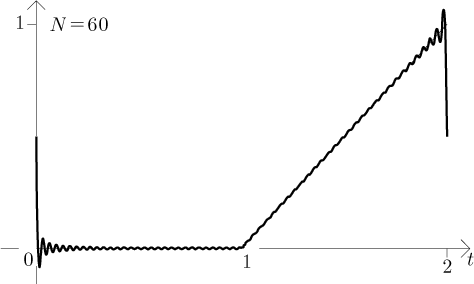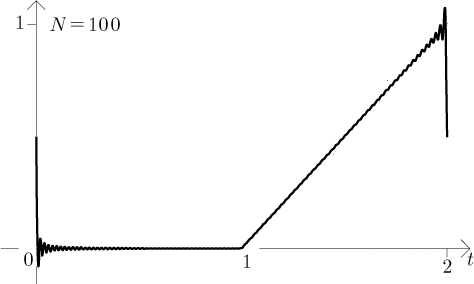
Řada se tedy chová přesně, jak bychom čekali podle Jordanových podmínek, třeba vidíme, že v bodech nespojitosti jde k průměru. Všimněte si oscilace okolo bodů nespojitosti. Jak se stupeň trigonometrických polynomů zvyšuje, tak jsou tyto oscilace omezeny na stále užší oblast okolo nespojitostí, ale magnituda těchto oscilací se nezmenšuje. Říká se tomu Gibbsův jev a děje se to nutně v situacích, kdy se snažíme Fourierovými řadami aproximovat nespojité funkce.
Připomeňme, že jsme také našli sinovou Fourierovu a kosinovou Fourierovu řadu. Máme tedy tři možné řady, jejich částečné součty stupně 15 jsou
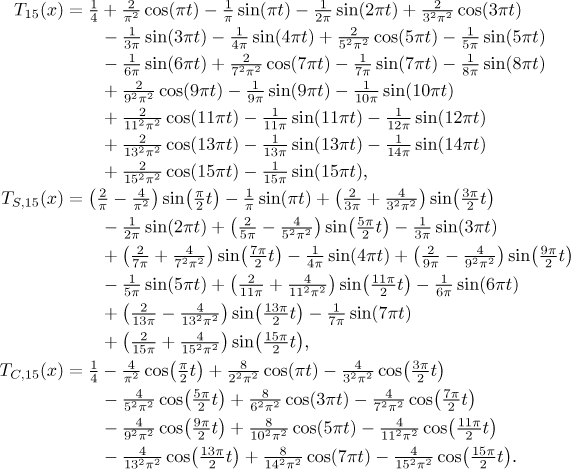
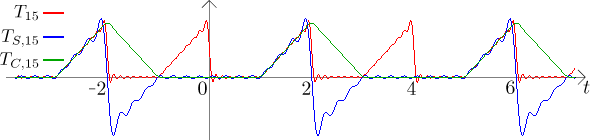
Víme, že sinová Fourierova řada konverguje k lichému periodickému rozšíření a kosinová Fourierova řada konverguje k sudému periodickému rozšíření (a průměruje v bodech nespojitosti). Následující obrázek ukazuje, že v našem případě ony 15. částečné součty evidentně vykazují toto chování.
Zase se soustředíme na
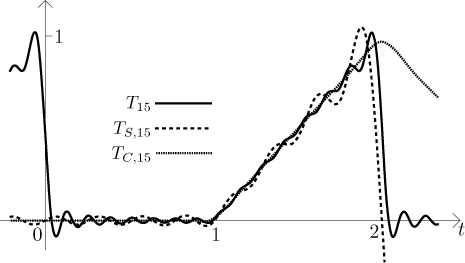
Na první pohled toto může být trochu překvapivé. Protože sinové a kosinové řady mohou pracovat s méně funkcemi, dá se čekat, že je pro ně těžší dosáhnout dobré aproximace, tedy čekalo by se, že budou konvergovat pomaleji než "opravdická" Fourierova řada. To se zdá být pravda pro sinovou řadu, ale kosinová Fourierova řada vypadá nečekaně dobře. Zde je důvod. Všimněte si, že sudé periodické rozšíření dané funkce je spojitá funkce, tudíž kosinová řada - i když má k dispozici méně funkcí - má zároveň mnohem snažší práci, protože se nemusí vypořádávat s nespojitostmi. To souhlasí s teorií, víme, že pro spojité funkce (a po částech spojitě diferencovatelné) dostáváme mnohem lepší konvergenci (je dokonce stejnoměrná).