Basic systems of functions

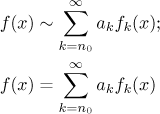
We start with an interesting result. First we state it in a classical form.

Theorem (Stone-Weierstrass theorem).
Let f be a function on a bounded closed interval I. If it is continuous, then for every ε > 0 there exists a polynomial P such that | f (x) − P(x)| < ε for every x from M.

That is, every continuous function can be approximated arbitrarily well by polynomials on bounded closed intervals. Now we will state it in a different language.

For every function f that is continuous on a bounded closed interval M there exists a sequence of polynomials {P_n} such that P_n ⇉  f on M.

While this theorem is very useful, it has one drawback. When we require better and better approximation, we usually need higher degree of P_n. However, the above theorem does not guarantee that a "longer" polynomial shares its beginning with a "shorter" polynomial, like it happens with the Taylor polynomial when we use a common center a and just change its degree. From this point of view the above theorem is not sufficient and we use the Taylor case as an inspiration for the following topic.

We are interested in Stone-Weierstrass approximations and Taylor polynomials for a simple reason. We would like to replace a given function that is perhaps not very pleasant by a function that we like without loosing too much. What does it mean, a "function that we like"? Usually we start with a set of nice and also simple functions, that is the basis for our work, and by "functions that we like" we mean all functions that can be obtained as linear combinations of that basic set. For instance, when approximating by polynomials, the basic system would be all powers x^k and their linear combinations are exactly the polynomials. Now we will put this down more precisely.

Given a set M (for simplicity we will assume that it is an interval), consider the set V of all functions defined on M. Then V is a linear space. We will consider a sequence of functions { f_k} from V that forms a linearly independent set. This will be the basic system of choice and its independence means that it is not needlessly large, all its functions contribute. The first step is to consider the linear subspace that these functions generate. For instance, if we take the popular example f_k(x) = x^k, then the linear subspace that this space generates is exactly the space of all polynomials. We already saw that this space is large enough to approach arbitrarily close every continuous function on M in case M is bounded and closed.

This brings us to the main object of interest. As we noted above, we prefer the situation when improving the quality of approximation means adding extra terms to an already existing approximation. This means that given a basic system { f_k}, we are interested in the space of all "infinite linear combinations", that is, the space of all convergent series of the form  ∑ a_kf_k. We then want to identify or describe this space. This usually means answering some crucial questions.

What are these important questions? Given a linearly independent set of functions { f_k}, we want to know the following:
 •  What functions f can be obtained as a sum of series  ∑ a_k f_k?
 •  If f = ∑ a_k f_k, how do we find the appropriate coefficients a_k?
 •  If f = ∑ a_k f_k, is the convergence uniform? Is it absolute?

In concrete situations these questions are usually extremely difficult to answer, even for nice systems. Very often we proceed as follows:

• We are usually able to specify some convenient space of functions for which we can guarantee that they can be expressed as  ∑ a_k f_k. We also usually know that there are also other functions for which this can be done, so we in fact rarely answer the first question above, in particular because once we move outside this convenient space, things get really technical and ugly. Therefore we are (at least from practical point of view) usually willing to settle for a space that perhaps does not exactly answer our question, but is nice and things work well there.
• We can also usually prove that if we have f = ∑ a_k f_k, then necessarily a_k must be given by a certain specific formula. Such a result is interesting from two points of view. First, it gives us uniqueness of expression as series, which is important from theoretical point of view. Second, it tells us that if we want to express some function as a series, then the coefficients given by this formula are the only candidates, because no other coefficients can work.
• Then there is a crucial question. If we are given a reasonable function f (from that convenient space discussed in the first item) and find coefficients a_k according to the formula from the previous item, does the resulting series  ∑ a_k f_k  actually converge to f?
  Note that this does not follow automatically, since the implication in the previous item goes in the opposite direction, and the answer is surprisingly often negative.
  

When working with these basic systems of functions, we therefore often see the following notation.

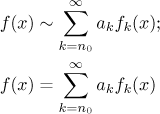
The first line means that we took f and created the coefficients a_k according to a specific formula that we found in the "wrong implication". Therefore this notation does not guarantee that the sum of the resulting series is in fact equal to f from which it came.
The second line means that f is equal to the sum of a certain series. Note that if we did not prove a result on uniqueness, then this series need not necessarily come from that specific formula.

In the subsequent sections we will explore two useful basic systems of functions. First we look at the system given by x^k (power series and Taylor series). This system is used to approximate "nice" functions and it is probably the most widely known system. The second system (Fourier series) is based on functions sin(kt) and cos(kt), it is rather good at coding functions that are not exactly "nice" (functions with discontinuities) and has many applications in signal processing, coding etc.

Power series
Back to Theory - Series of functions