Theorem.
Let
Let c be any real number, let f and g be
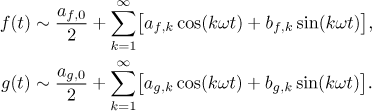
Then
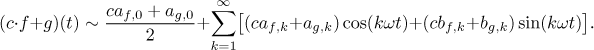
Here we will look at the usual properties we ask from series expansion (how it behaves with respect to the usual operations and how it reacts to transformations of functions). Then we look at alternative ways to write Fourier series, namely the amplitude - phase angle form and the complex form.
We start with a result that is not related to the main topic of this section, but it is sometimes useful, so we quickly go through it.
Theorem.
LetT > 0, denoteω = 2π/T.
For anyT-periodic function f that is integrable on[0,T ], the Fourier coefficients ak and bk tend to zero.
Now we turn to investigation of operations. First one fairly obvious result that follows from the fact that coefficients of Fourier series are given by integrals, that is, by a linear process.
Theorem.
LetT > 0, denoteω = 2π/T.
Let c be any real number, let f and g beT-periodic functions that are integrable on[0,T ]. Assume that
Then
Now we would like to determine similar formulas for derivative and integral.
With derivative it is simple. Assume that f is
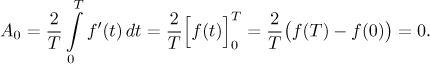
The integrals for the other coefficients can be changed into integrals featuring f using integration by parts.
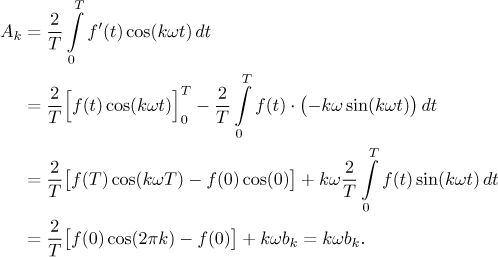
Similarly we evaluate bk and obtain the following statement.
Theorem.
LetT > 0, denoteω = 2π/T.
Let f be aT-periodic function integrable on[0,T ]. Assume that
Then
So we see that we can differentiate both sides of the "tilde relation" (the Fourier series we differentiate term by term) and the relation stays valid. How about a true equality? If we use the usual Jordan conditions (but applied to f ′), we get the following implication:
Assume that f is piecewise continuous and has the first and second derivative that are piecewise continuous. Then
That is, we can differentiate a convergent Fourier series term by term. Now
we turn to integration. We again start with formal assignment of Fourier
series, that is, assume that f is
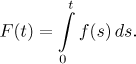
Now consider some t from the interval
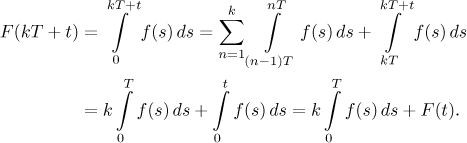
We see that this antiderivative F is
Antiderivatives of f areT-periodic exactly ifa0 = 0.
Under this assumption we may start asking about the Fourier series assigned
to F. This time coefficients are given as integrals with F and
we use integration by parts to pass to integrals with f, then we use
periodicity of f and also the fact that our special F has
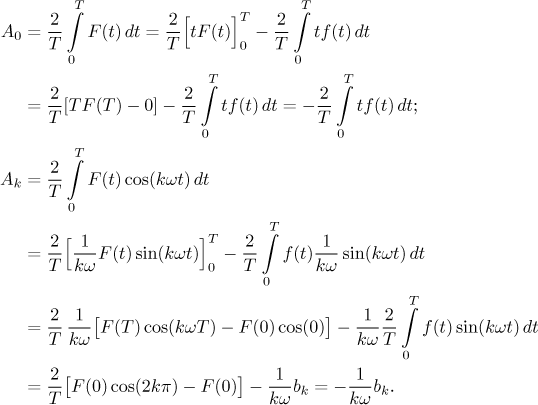
Similarly we evaluate the integral for Bk. Thus we get the following statement.
Theorem.
LetT > 0, denoteω = 2π/T.
Let f be aT-periodic function continuous on[0,T ]. Assume that
If a0 = 0, then for the antiderivative given by
we have
This tells us about one particular antiderivative. Other antiderivatives differ by a constant, so if we consider the set of all of them (the indefinite integral), we can write the conclusion in the following way:
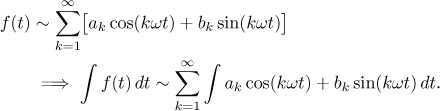
How about true equality instead of formal assignment? Again, we will use Jordan's conditions. We need to guarantee that an antiderivative exists, for which the natural assumption is that f is continuous. The antiderivative F in the above theorem is then also continuous, therefore F and its derivative f satisfy the "better" version of assumptions in Jordan's theorem and we actually get uniform convergence.
Instead of expressing this formally we will try something else, we look at
definite integral (which is in a sense more general). Since we will not work
with antiderivatives, we do not have to worry about their periodicity and
thus we need not require that
Theorem.
LetT > 0, denoteω = 2π/T.
Let f be aT-periodic function that is piecewise continuous and integrable on[0,T ]. Assume that
Then for any a < b we have
Now we will look at how Fourier series reacts to transformations of f. Note that if f is a periodic function, then the usual transformations again yield periodic functions, and apart from scaling the variable they even preserve the original period.
Theorem (transformations).
LetT > 0, denoteω = 2π/T.
Let f be aT-periodic function that is integrable on[0,T ]. Assume that
Then for any non-zero real number c we have
The first statement we already saw above, it follows from linearity.
Note that a0 is actually the average of f
(multiplied by 2), so by scaling the variable (shrinking or expanding the
function along the
Note that this last formula looks much better in complex form, see below.
The basic Fourier series can be rearranged to better suit one's needs. The first rearrangement that we will show here uses a trick that is fairly popular when working with waves (signals, electrical circuits etc.). Given numbers a and b, there is a certain angle φ and a number A such that for any x we have
![]()
The number A is called the amplitude and the angle φ is called the phase angle, they are given by the following formulas.
![]()
If we exchange sine and cosine in this definition of φ, we get a similar reduction, but this time with cosine on the right (the phase angle will be now different). If we apply this to all terms in the Fourier series, we get the following formulas.
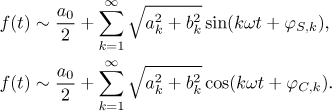
Here we use a different trick. If we replace sines and cosines in a Fourier series by their equivalent expressions with exponentials, we get
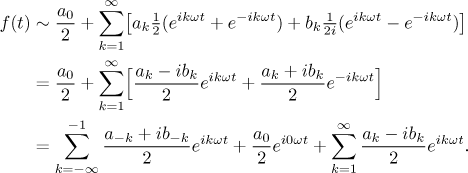
Thus if we denote
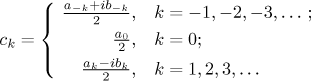
we get the complex form of Fourier series
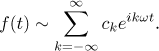
This form is actually the natural form of this series, since many formulas become much nicer. For instance, we do not have to find ck by doing several cases, there is a common formula for them all:
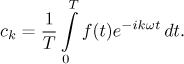
Indeed, for instance, for a positive integer k we have
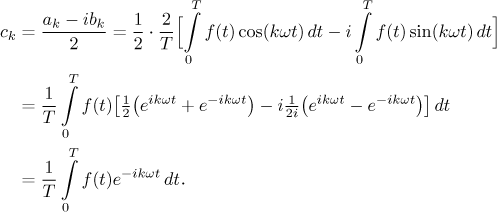
Similarly, there are more convenient forms for the rules for transformations above.
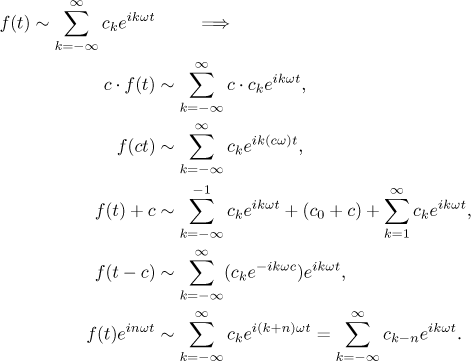
In the last formula, n is obviously some integer.
Going a bit further in this direction would get us to the notion of Fourier transform, which is another story, so we'd better stop.