Convergence of power series: Methods survey

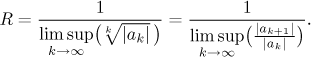
When given a power series, we know that it converges on some neighborhood of its center (perhaps including some endpoints of this neighborhood). Its convergence can be therefore described by providing these basic parameters: The center, the radius of convergence, the region of absolute convergence, and the region of convergence. Sometimes we are not all that much interested in what happens at endpoints, then the first two pieces of data (center and radius) are considered sufficient.

1. Determining center. This is actually very simple. The "official" form of a power series features terms (x − a)^k and this a is the center. Thus the only minor complication may arise if a series is given in another way, but this is simple to fix using algebra (see Example below).

2. Determining radius of convergence. This is done by investigating absolute convergence of the given series.
Step 1. Apply absolute value to terms of the series and simplify, in particular you should get the term |x − a|^k in it.
Step 2. Apply either the Root test or the Ratio test to this series. The corresponding constant in most cases (but not necessarily) features |x − a|.
Step 3. Check on convergence by solving ϱ < 1, respectively λ < 1. If the term |x − a| appears in this inequality, then you should be able to deduce an inequality of the form |x − a| < R. This R is then the radius of convergence.
If the term |x − a| does not appear in the condition on convergence, then in a typical case either the corresponding constant (rho or lambda) is zero, which gives radius infinity, or the constant is infinity (apart from the center), which gives radius zero.

Alternative: Some people prefer to use the formula

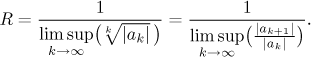
Its disadvantage is that it can be used only for series in the "official" form, whereas the procedure described above can be also applied to series in different forms (see Example below).

3. Determining behavior at endpoints. Endpoints are a − R and a + R. To find out about convergence there, simply substitute each of them into the given power series. You always get a series of real numbers whose convergence can be investigated using the usual procedure, see Methods Survey for Testing convergence. Note that it is pointless to use the Root test or the Ratio test, they must come inconclusive (since the radius from part 2 is exactly the place where these two tests stop giving information).
Note that this only applies to the case of positive R, there are no endpoints when R is zero or infinity.

4. Regions of convergence. If the radius of convergence is positive, then the region of convergence is the interval given by the center and the radius, (a − R,a + R), with endpoints that in previous step lead to convergent series included.
Usually the open interval above is also the region of absolute convergence. The only exception is the case when we get convergence at both endpoints, in which case the region of absolute convergence is usually the closed interval as above and it coincides with the region of convergence.
If R = 0, then the region of convergence and the region of absolute convergence coincide, it is the one-point set {a}.
If R = ∞, then the region of convergence and the region of absolute convergence coincide, it is the set of real numbers.

Remark: Often we are given a power series that is not in its proper form, which usually means that instead of (x − a)^k it features terms (Ax − B)^k. It is simple to rewrite such a series to the proper power series form and then use the above algorithm (see Example below), but usually it is faster to apply the above procedure to the series as given.

Example: Investigate convergence of the series

First we rearrange the series so that it has the proper form.

Thus the center is a = −2. Now we apply absolute value to the terms of this series and try the Root test to determine convergence. We use A_k in the formula of the Root test since in the context of power series, the notation a_k is usually reserved for coefficients, not whole terms of the series.

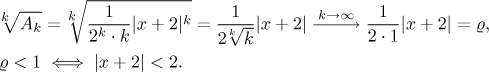
Thus we get the radius of convergence R = 2.

From the center and radius of convergence we see that endpoints are −4 and 0 (see picture below), now we check on them.

x = −4: We substitute into the given series (as we rewrote it above) and obtain

This is the famous alternating harmonic series that is known to converge by the Alternating series test, see the example there.

x = 0: We substitute into the given series and obtain

This is the equally famous harmonic series that is known to diverge (or we apply the p-test).

Conclusion: The region of convergence is the interval [−4,0), the region of absolute convergence is the interval (−4,0).

Some people find it easier to work with these notions if they draw a picture and fill in data at every step.

Remark: The series in the above example was not given in its proper form, how would we apply the above algorithm to this series as given?

The center is found by solving the equation 2x + 4 = 0.

The constant ϱ is found similarly as above.

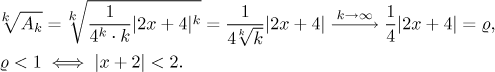
This way it is usually easier. However, if you are used to determine the radius of convergence using that formula, then you necessarily do have to change the series to its standard form.

For other examples see Solved problems - Series of functions.

Expanding in power series
Back to Methods Survey - Series of functions