Root test: Methods survey

The Root test is used as follows.

Algorithm:
We are given a series  a_k  with non-negative terms.
Step 1. Evaluate the limit

Step 2. Assume that this limit exists.
• If ϱ < 1, then the given series converges.
• If ϱ > 1, then the given series diverges.

This test is obviously perfect for series whose term are of the form (c_k)^k, but it can also handle polynomials well due to the following handy fact.

If p(x) is a non-zero polynomial, then

Note, however, that the case ϱ = 1 is indecisive, so polynomial parts do not help to decide convergence in the Root test; in order to reach a conclusion, there must be also parts of different kind (like c^k or those factorials) in the given series.

Example: Decide on convergence of the series

The denominator just calls for the Root test. Using the fact above we get

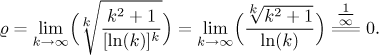
Since ϱ < 1, the given series converges.

For other examples see especially this problem, this problem, and this problem in Solved Problems - Testing convergence.

Sometimes one has to use more general (and less convenient) versions of the Root test, see Root and Ratio test in Theory - Testing convergence; for an example see this problem in Solved Problems - Testing convergence, also look at this problem.

One can also use this test to get some information about series with general terms, not just non-negative, see the Note at the end of the section Root and Ratio test in Theory - Testing convergence.

Ratio test
Back to Methods Survey - Testing convergence