Summing up (power) series: Methods survey

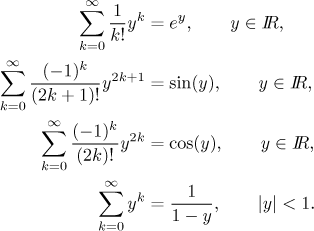
We are given a function series ∑ f_k(x) and we want to find its sum (if possible). There are no general methods for doing this, but one particular approach may often help. The basic idea is that we try to make the given series look like a series that we already know - taking into account the fact that we can do substitutions. In most cases we use this for power series, but substitution allows us to apply this idea also to other series (if we get lucky).

The more series we know to start with, the better our chances to succeed, but usually the starting points are these four.

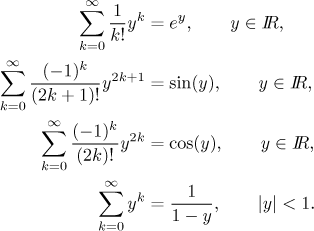
It is also good to know series for logarithm.

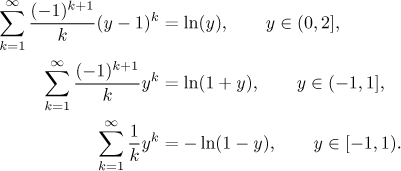
However, one can do without them, in case you are willing to work more: Such series can be transformed to geometric expansions using derivative.

Algorithm: The procedure starts by writing an equality, where on one side you put the given series and on the other side you put the symbol f (x). Now apply various transformations to both sides of this equality so that out of the given series you eventually create a series that you know, this you can replace with an explicit function. Then solve the resulting equality for f.

The are two things one usually has to do.

Step 1. The parts of f_k that feature x should be written as [g(x)]^k, where g(x) is an expression that is common to all f_k. The basic tools are smart bracketing and shifting power by factoring things out of the series or bringing things into series. Some simple examples:

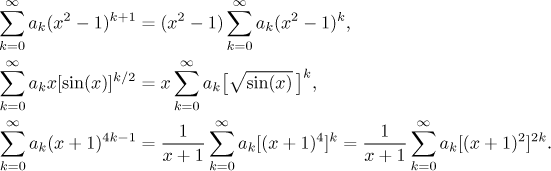
Note that in the last example we offered two possibilities, since one can try to fit this series also to the series for cosine. Whether this is a good idea or not depends on the coefficient a_k. If we can transform it so that the factorials (2k)! appear in the denominator (see the next step), then going for cosine might be the right idea. Or for sine - we saw that shifting the power up or down by 1 is no problem; this all depends on the coefficients and what are we able to create there. In fact, all terms with power k can be transformed to power 2k or some other multiple of k and vice versa as in the above examples; we have some freedom here and coefficients should guide us which way to go, see the next step.

Step 2. The coefficients should be fixed so that they have the right form. There are five basic operations one can use.
• If the coefficients have the form of sum, the series can be split in two.
• Unwanted constants that do not depend on k can be factored out.
• Expressions A^k can be included in the x part.
• Expressions like k, k + 1 etc. in the denominator can be removed when you differentiate the series - but you have to fix the power at the x part properly, we learned in Step 1 how to shift it. For instance, if you want to remove k − 1 from the denominator, you have to first fix the x group so that it has the form [g(x)]^k−1 and then differentiate.
• Expressions like k, k + 1 etc in the numerator can be removed when you integrate the series - but again you have to fix the power at the x part. For instance, if you want to remove k − 1 from the numerator, you have to first fix the x group so that it has the form [g(x)]^k−2 and then integrate.
There is no reasonable way to remove/add factorials, so if they appear in the given series, they pretty much determine which way we should go - note that the above four series have different kinds of factorials.

Step 3. When the series has the right form, one has to make sure that indexing actually starts at the right place, the subtract/add trick is used for it (see Manipulating (power) series in Methods Survey - Series of functions).

Notation: There are essentially two ways in which to proceed. There is a general way, the one described above, when you start with the basic equality featuring the given series on one side and " f (x)" on the other side and you keep working on this equality until you can replace the series with a formula. However, sometimes this is unnecessarily complicated. In case you can only use operations that do not change the series itself, just change its appearance (this above all means that you do not plan to use differentiation and integration), then you can use a simpler notation. Start with the given series and by a chain of equalities you bring it to a form that you can already sum up.

We will now show an example. It is a bit beastly, since we wanted to show what can be done. For more reasonable examples see Solved Problems - Series of functions.

Example: Find the sum of the series

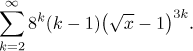
Since there are no factorials, there is no way to change this series into a series for the exponential, sine, or cosine. Thus we will try to make it look like the geometric series, we will use the general notation with  f discussed above. First we get rid of the 3 in the power, then we move the term 8^k into the x-part.

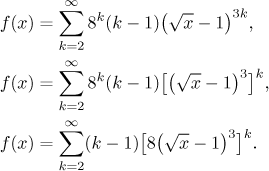
Now we need to get rid of k − 1, so we prepare the appropriate power and integrate.

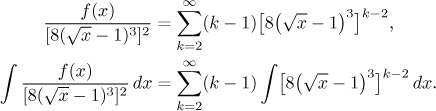
We see that we cannot figure out the integral on the right, so we have to go back a bit and prepare the series more carefully. We put in some terms that will allow us to use the natural substitution for integrating.

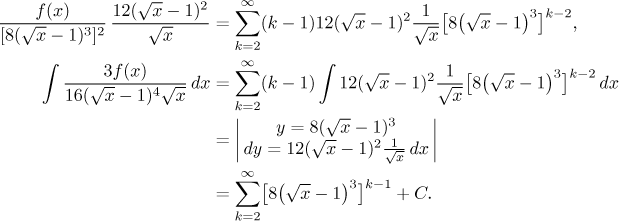
Now we again fix the power in the x-term and then apply the factoring out trick that makes the indexing of a geometric series start from 0. Then we can use the geometric expansion.

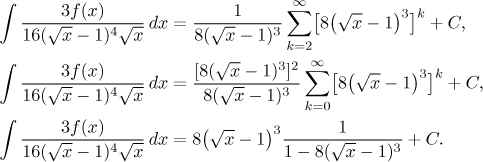
Note that this geometric expansion is true only if the term that was taken to power k is less than 1 in absolute value. This will determine the validity of the result. Now it remains to solve for f.

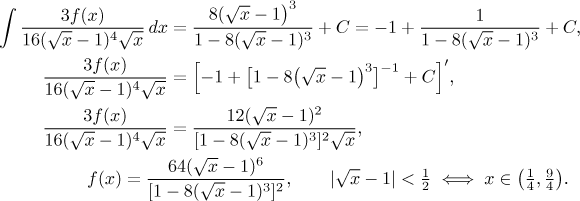
By the way, on the first line we did this: We denoted the whole third power as A, then we used my favorite add-subtract trick.

Remark: Of course, for many series these tricks do not help at all. Sometimes they do work to give a nice series, but trouble starts later, when solving for f. As an example we briefly show one deceptively simple series that we would really like to sum up.

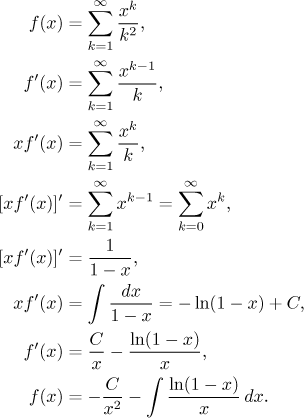
And that is the end of the road, we do not know how to explicitly express the integral on the last line.

Expanding in Fourier series
Back to Methods Survey - Series of functions