Problem: Investigate convergence of the following sequence of
functions:
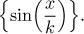
Solution:
First we investigate pointwise convergence. We treat x as a parameter
and evaluate limit with respect to k. Then the argument of sine goes
to 0 and since sine is a continuous function, we get
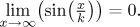
Conclusion: The given sequence converges to the function
f (x) = 0 on the whole real line (which
is thus the region of convergence of this sequence).
How about uniform convergence? We start by investigating the difference
between f and a particular fk on the above
region of convergence.
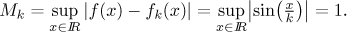
We have just proved that uniform convergence does not work on the whole
real line, since the suprema do not go to zero.
Is there a way to avoid this trouble? Yes. We know that
|sin(y)| is sometimes small and sometimes large, and at
the origin it starts at level 0. The closest number to the origin when this
function is equal to 1 is y = π/2. If we stay
significantly closer to the origin than this number, then sine does not
become large. In our setting, the nearest point to the origin where
sin(x/k) is equal to 1 is
x = (kπ)/2. Note that as we
increase k, these points move away from the origin. Thus if we
consider a concrete interval around the origin, then sooner or later those
critical points leave this interval and sine starts being small there.
One can also use pictures to see this idea. Note that the functions
fk are all just sines with scaled variable and the
scaling actually stretches the sine out.
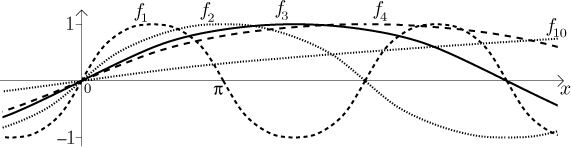
Thus we indeed see that each of these functions are always too large some
place and thus does not approximate f(x) = 0
well, but those humps happen further and further from the origin. We
therefore guess that the right sets for uniform convergence are sets of the
form M = [−a,a] for
a > 0. We want to evaluate
Mk for such a set. Note that once a is
fixed, then for all k satisfying
k > a, the functions
fk are increasing on M and also symmetric
there, so we get
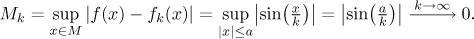
Thus our guess is confirmed, the suprema go to zero.
Conclusion: The given sequence converges to the function 0 uniformly
on sets of the form
M = [−a,a] for
a > 0.
Next problem
Back to Solved Problems -
Series of functions
![]()
![]()
![]()

![]()