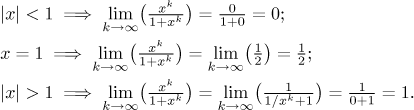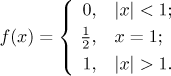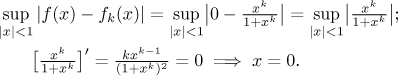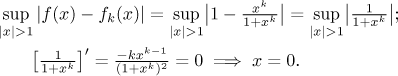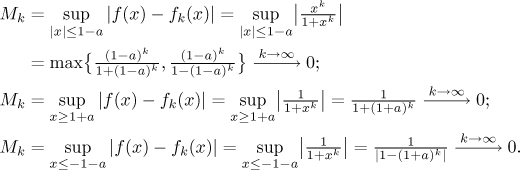Problem: Investigate convergence of the following sequence of functions:

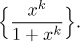
Solution: Before we start, note that the point x = −1 is not in the domain of functions with odd k, therefore we exclude it from all our considerations right away.

First we investigate pointwise convergence. We treat x as a parameter and evaluate limit with respect to k. When we send k to infinity, then the limit of x^k depends on x, see geometric sequence. Therefore we have to adopt three distinct strategies when evaluating this limit. For |x| < 1 the terms x^k disappear; for |x| > 1 they become dominant and the best approach is to get rid of them by canceling; when x = 1 then all functions have the same value and we get a constant sequence.

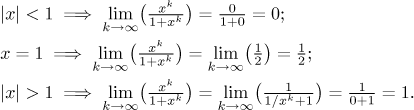
Conclusion: The given sequence converges on the region of convergence consisting of all numbers except x = −1 to the function

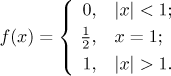
How about uniform convergence? We start by investigating the difference between f and a particular f_k on the above region of convergence. Again, we have to do our exploration separately on three regions. First, at x = 1 the difference is always zero. For |x| < 1 we get

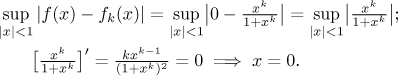
The critical point x = 0 is obviously a local minimum of the given function (in absolute value), so the supremum is given by values at endpoints. The limit at 1^- yields 1/2, so the supremum is at least 1/2 for all k and therefore we cannot get uniform convergence on (−1,1). Note that things get equally bad at −1. If k is even, then the limit at (−1)⁺ is again 1/2, but if k is odd, the limit there is actually minus infinity!

Uniform convergence on the whole region of convergence has just been ruled out, but to get the whole picture we also check on the two intervals given by |x| > 1.

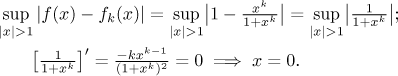
We see that the expression in the supremum is increasing for x > 1 and monotone for x < −1 (increasing if k is even, decreasing for k odd). The supremum is therefore given by values at endpoints. Limit at infinity and minus infinity is 0, so there is no problem. Limit at 1⁺ is 1/2, so the supremum over x > 1 is 1/2 and uniform convergence is ruled out there. Finally, also for x < −1 we do not get uniform convergence, the limit (and supremum) being either 1/2 (for k even) or infinity (for k odd).

We see that uniform convergence is hurt by behavior of the given sequence on both sides of 1 and of −1. This suggests that if we cut away these points, then we do get uniformity. Our observations about monotonicity suggest that when we choose some a > 0 (and for the middle interval to work a must be small, less than 1), then we should get uniform convergence on intervals M = (−∞,−1-a], M = [−1+a,1-a], and M = [1+a,∞). We confirm this by evaluating the corresponding suprema for these three sets.

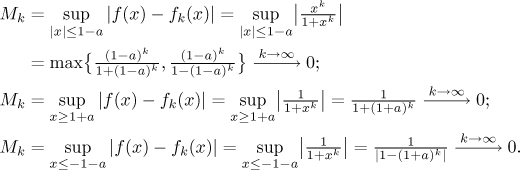
Conclusion: The given sequence converges to the function f uniformly on sets of the form M = (−∞,−1-a], M = [1+a,∞), M = [−1+a,1-a] for any a > 0 (in the last case we also require that a < 1).

For illustration we show a picture with some of the functions.

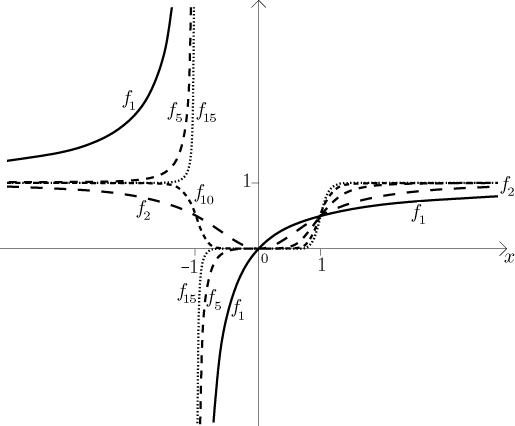
Next problem
Back to Solved Problems - Series of functions