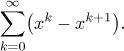
Problem: Investigate convergence of the following series of functions:
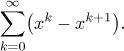
Solution: First we investigate pointwise convergence. We treat x as a parameter and test convergence of the resulting series of real numbers. In a typical case we would test absolute convergence using some tests, we show this approach in this note. However, this approach, while more general, yields less information, in particular it does not tell us what a sum of a series is. Usually we accept this limitation and go to tests right away, why not here?
If they did not expect us to do something with the sum of this series, just work out convergence, then they would have given this series without indexing limits, since they are irrelevant when we just check on convergence. The fact that those limits are there is a clear hint. We therefore need a better tool and we do have one, since the given series is obviously a telescopic series. Thus we proceed by evaluating partial sums of this series and then passing to the limit with N.
Note that for those x where this series converges, the terms of this series are non-negative. This means that this convergence we just proved is also absolute.
Conclusion: The given series converges and converges absolutely
on the region of (absolute) convergence
![]()
How about uniform convergence? We start by investigating the difference
between f and a certain partial sum sN on the
above region of convergence. Since the case
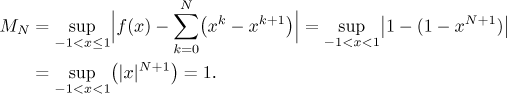
Since the supremum does not go to zero for N going to infinity, we do
not have uniform convergence. However, we also see that the trouble happens
at 1 and at −1, so we expect that if we cut them off, we already get good
approximations. To this end, consider a set of the form
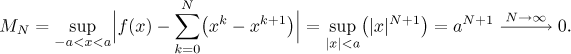
Conclusion: The given series converges to the function f
uniformly on sets of the form