Problem: Investigate convergence of the following series of functions:
![]()
Solution: First we investigate pointwise convergence. We treat x as a parameter and test convergence of the resulting series of real numbers. Since cosine hyperbolic is always positive, the given series has non-negative terms and we can apply suitable tests to work out its convergence (that is also absolute convergence).
What tests seem good here? Taking the
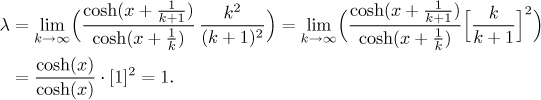
Thus the test was inconclusive. What other test can we use? There is only
one reasonable choice,
limit comparison. We see that
for large k, the numerator is essentially equal to
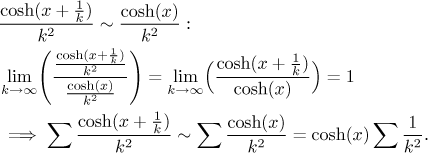
Since the series on the right converges (see the p-test), also the series on the left converges. Note that this convergence does not depend on x.
Conclusion: The given series converges (absolutely) on the whole real line (which is the region of (absolute) convergence).
How about uniform convergence? Since we do not actually know the sum of
the given series, we cannot use direct methods. However, the comparison above
suggests that the
Weierstrass test should work fine
on bounded sets. Indeed, fix any A < B and
consider the set
![]()
Therefore
![]()
Since the series
Conclusion: The given series converges uniformly on any bounded closed interval.