Problem: Investigate convergence of the following power series:

Solution: This looks like a straightforward problem, so we use the standard approach. First we rewrite this series into its standard form.

We see that the center of this power series is a = 2. Now we determine its radius of convergence by testing its absolute convergence. We use a suitable test, here the Root test should work well.

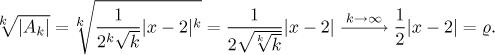
We used notation A_k for terms of this power series, since "a_k" (that you usually find in the Root test) is used for coefficients in the context of power series.

We know that the series converges absolutely if rho is less than one, thus the condition is |x − 2| < 2.

We see that the radius of convergence is R = 2.

The interval of convergence is therefore at least

(2 − 2,2 + 2) = (0,4).

What is unclear is the status of endpoints, we need to check on them individually.

Endpoints:
x = 0: We substitute into the given series (which is usually better than substituting into the "proper" form) and obtain the series

This particular series is actually something that we should know, since it is a p-series. In this case p = 1/2 < 1, therefore this series diverges. The point x = 0 is not in the region of convergence.

Note that this x lies exactly on the border of the region determined by the radius of convergence, so it would yield 1 when substituted into the formula for rho above. Thus there is no point in trying the Root test or the Ratio test on this series.

x = 4: We substitute into the given series and obtain the series

What test do we use? Since the terms are not positive, we cannot use the usual tests. The natural choice here is the Alternating series test with

The sequence {b_k} is positive, decreasing and tends to zero, consequently the series in question converges. The point x = 4 does belong to the region of convergence.

Since at least one endpoint is missing from the region of convergence, it follows that we cannot have absolute convergence at them.

Conclusion: The given series has the center a = 2 and radius of convergence R = 2. Its region of absolute convergence is (0,4), its region of convergence is (0,4].

Remark: It is not really necessary to rewrite the series to its "proper" form. The center can be found by solving

(x/2 − 1) = 0.

Also the Root test can be applied to the original form of the series, then at the very end we do have to rewrite the resulting expression so that there is no multiplicative constant with x in the absolute value. The resulting rho should be the same. Indeed,

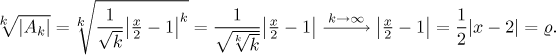
Thus it seems that it is in fact easier to work with the given series as given, we save one step in solution. In most cases this is fine, that extra step serves one purpose: It confirms that we indeed work with a power series, therefore our procedure is justified. Since this is usually quite obvious, I usually opt for the faster way.

Remark: Some people prefer to determine the radius of convergence in a different way, namely they remember the formula from the appropriate Theorem. Their calculation would go like this.

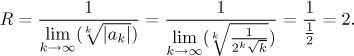
We skipped some steps in this calculation, since they are obviously the same as above. Both ways (application of the Root test or using the formula from Theorem) have a common core, it is a matter of personal taste which one is better. Note that this calculation with formula does require that we rewrite the given power series into its standard form. This is one reason why I prefer to use the Root (or Ratio) test as shown in the first Remark, then I save the step of rewriting the given series. The second reason is that I need not remember the special formula, just the Root test (or the Ratio test) which I remember anyway.

Next problem
Back to Solved Problems - Series of functions