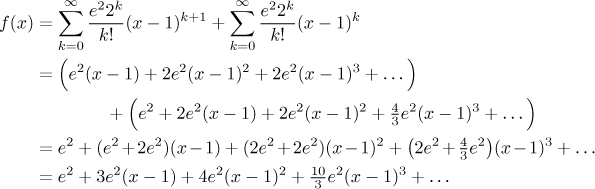Problem: Expand the given function in a power (Taylor) series with the given center:

Solution: We use the standard approach. We see that once we expand the exponential, our main work is done, the remaining parts are easy to handle. Thus the given function already has a reasonable form and we can pass to the first step, changing all x so that instead we have terms (x − 1).

If we expand the exponential now, the resulting series will have terms as in its argument, so it will not be a power series with center 1. Thus we need to get rid of the "+2" in the exponential, this is simple using algebra. Similarly we have to get rid of the "+1" in the term in front of the exponential, so we split that expression in two.

Now we are ready to expand the exponential using the series for e^y, then we rearrange the resulting series so that the terms (x − 1) appear in it. We also use distributive law to move terms that are in front of exponentials inside the resulting series.

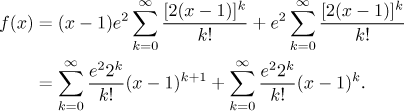
Note that the exponential expansion is valid for every y = 2(x − 1), from which it follows that the result is true for all x.

We have the answer expressed as a sum of two power series, but it is expected that we provide one power series. Thus the last step is to put the two series together. Note, however, that if we add them, we get a series in which different powers of (x − 1) appear and thus we will not be able to rewrite it as a power series. Thus we first have to reindex the first series so that the exponent in the power is also k, this is done by shifting the index up by 1. Formally we introduce another index (say, n) given by n = k + 1 and then we return to the traditional k by simple replacement.

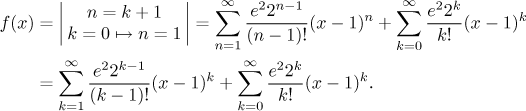
Now both series have the same power at x, but they have different indexing. We see that the second summation has one extra term (when k = 0), so we take it away from this series. Then we can add the series and (after making the resulting sum somewhat nicer) we arrive at the "perfect" answer.

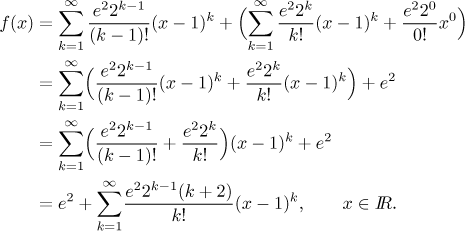
Remark: What is the point in making one series, when it took us so much work? When working with series, one often needs to know what is the coefficient in front of, say, (x − 1)¹⁷. This is easy to see in our final answer, but if we left it as a sum of several series, then we would have to look through all of them for appearances of (x − 1)¹⁷ and add the corresponding coefficients to get it. Actually, this is what we did above in general, we put together corresponding powers from all places where they may appear. This procedure (which is quite hard for beginners) is much easier to grasp if we have some intuitive idea of what is happening. In other words, we can see it well when we write the series in the long way.

Next problem
Back to Solved Problems - Series of functions