Problem: Expand the given function in a power (Taylor) series with the given center:

Solution: We use the standard approach. What function will be the basic one to expand? There is no exponential, sine or cosine, so by elimination it is either the geometric expansion or some more advanced trick. Can we make it look like (roughly) the function 1/(1 − y)? We see that the main problem is the x in the numerator, but this can be got rid of using long division with remainder. So that's how we start, then we pass to the first step, changing all x so that instead we have terms (x − 1).

Now we follow the standard procedure to create 1 − y in the denominator. First we change "2" into "leading 1", then we fix the sign after it.

Now we are ready to expand this fraction using the geometric series, here we have to be careful about validity of that expansion. Then we rearrange the resulting series so that the terms (x − 1) appear in it. We also use distributive law to move terms that are in front of the series inside.

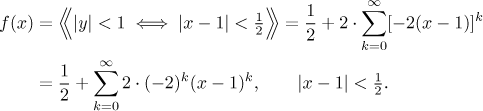
Note that the fraction 1/2 is actually also a series, namely a series whose term a₀ is 1/2 and all the other terms are 0, and these two series overlap, since also the second series contains some absolute term. In order to create just one power series we split the second series into two parts, its absolute term and the rest, and them put the two absolute terms together. At the beginning we also slightly rewrite the main series to make it look nicer.

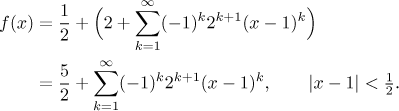
Bonus: The given function is actually a ratio of two functions that we know how to expand in power series, therefore we can try to expand this ratio using the method of undetermined coefficients. We write the numerator and denominator as series, which is quite simple. These are polynomials and thus we simply rewrite them to a form that features terms (x − 1). The resulting ratio is "nice" at 1 (we do not divide by zero when x = 1), therefore it can also be expanded in power series, we write it as a general series with coefficients a_k.

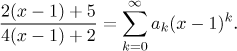
Now we multiply both sides by the denominator in order to get rid of the fraction and then rewrite the resulting series on the right into one series. Fortunately we do not need to use the Cauchy product there, since one of the two series is "finite", it has only finitely many non-zero terms.

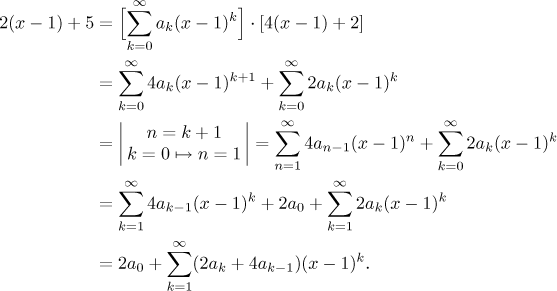
On the third line we shifted indexing in the first series to get the right power, then we had to take away the first term in the second series so that the two series on the right have the same indexing.

We obtained equality of two series, so by uniqueness of expansion the corresponding coefficients on the left and on the right must be the same.

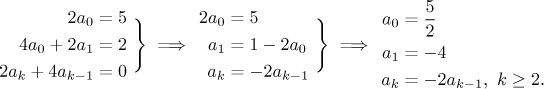
Using the last formula we recursively obtain a₂ = 8, a₃ = −16, a₄ = 32, we can guess and then prove by induction that in fact a_k = (−1)^k2^k+1. This is formally true for all k > 1, but also the coefficient a₁ fits this pattern. We therefore eventually obtain the same series that we have above.

Next problem
Back to Solved Problems - Series of functions