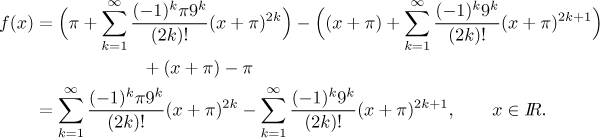Problem: Expand the given function in a power (Taylor) series with the given center:

Solution: We use the standard approach. We see that once we expand the cosine, our main work is done, the remaining parts are easy to handle. Thus the given function already has a reasonable form and we can pass to the first step, changing all x so that instead we have terms

(x − (−π)) = (x + π).

Here we go:

If we expand the cosine now, the resulting series will have terms as in its argument and it will not be a power series with center -π. Thus we need to get rid of the "−3π" in the cosine, this is simple using an appropriate identity. Similarly we have to get rid of the "-π" in the term in front of the cosine, so we split that expression in two.

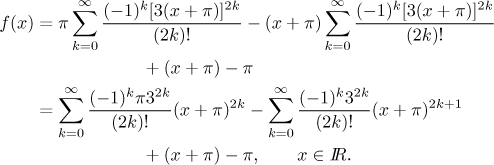
Now we are ready to expand the cosine using the series for cos(y), then we rearrange the series so that the terms (x + π) appear in it. We also use distributive law to move terms that are in front of cosines inside the resulting series.

Note that the cosine expansion is valid for every y = 3(x + π), from which it follows that the result is true for all x.

We have the answer expressed as a sum of two power series, but it is expected that we provide one power series. Thus the last step usually is to put the two series together. Note, however, that in this particular example it would be rather unpleasant, since one series features even powers and the other odd powers, therefore there is no overlap. If we really wanted to write it as one series, we would have to put in a general coefficient ak in there and then describe its value depending on whether k is even or odd, so we would not make things easier for the reader, they might be even worse. Therefore in such a case of non-overlapping series we traditionally keep them as they are.

Here we actually should do one thing, each series has a common term with the extra finite part, namely the power (x + π) also appears in the second series and the constant term appears also in the first series. Thus we can separate the appropriate parts from each series and put them together. But that's the best one can do.

Next problem
Back to Solved Problems - Series of functions