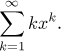
Problem: Sum up the following power series:

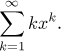
Solution: We need to convert the given series into a series that we already know. Since there are no factorials in this series and we cannot create them there, the series for the exponential, sine and cosine are out of question. Thus we should turn our attention to the geometric series (or logarithmic or binomial series, if we happen to remember them). None of these series has k in the numerator, so we definitely need to get rid of it. We know how to do such a thing: When we integrate a series, we divide terms by k + 1. Here we actually need k to appear in the denominator, which we get by integrating x^k−1. We even know how to obtain this in our series (we factor out x).

It seems that we have a plan how to change our series so that it only features x^k, that is, a geometric series that we know how to sum up. We denote the sum of the given series by f and proceed with our plan.

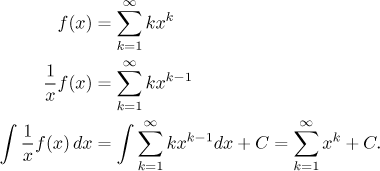
We almost have a geometric series, the only problem is the beginning of the indexing, but we have tricks for that, too. We can use the general add-subtract trick to fill in the missing term, however, for a geometric series we prefer to factor out the lowest term present in the series. Note that the calculations worked only for non-zero x.

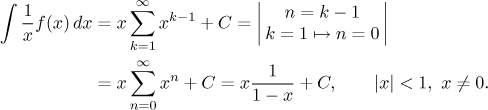
Now we solve this equation for f (x).

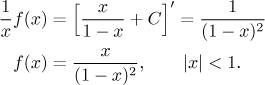
We did our calculations for x different from 0, but at the end we obtained two functions that are equal on an interval except a point in its middle; since these two functions are continuous, we also get equality at that one point.

Next problem
Back to Solved Problems - Series of functions