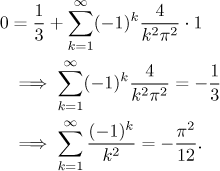Problem: Find the Fourier series and its sum for the following function:
![]()
Solution:
This seems to be a standard problem, so we use the
usual procedure.
When we extend the given function periodically, its period will be
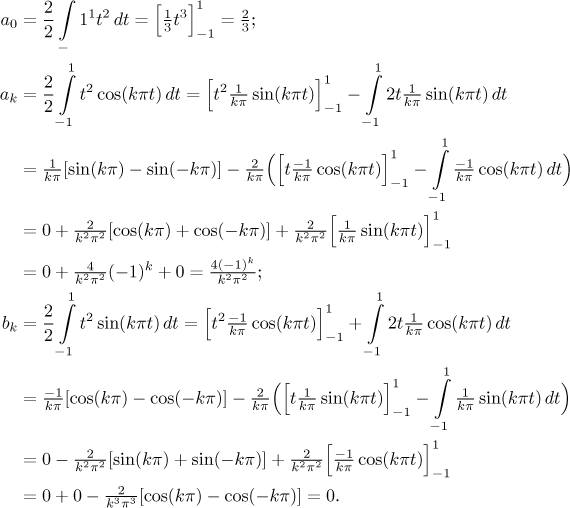
Since f is even, the fact that
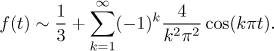
To find the sum of this series we use Jordan's conditions. First we draw the periodic extension of the given function f. Then we should check on points of discontinuity, but there are none. Thus the Fourier series converges to this periodic extension, and the convergence is uniform on the whole real line.

Remark: What do we get if we substitute
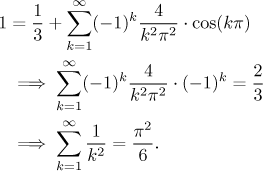
What do we get if we substitute