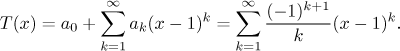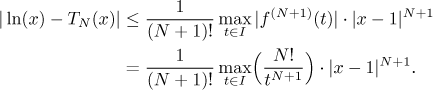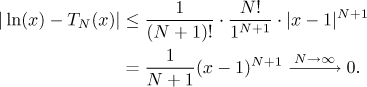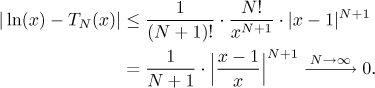Taylor series for the logarithm
We first derive the Taylor series for
f (x) = ln(x)
with center a = 1.
By induction it is easy to prove that for every natural number k, the
k-th
derivative is
f (k)(x) = (−1)k+1(k − 1)!/xk,
hence the coefficients are
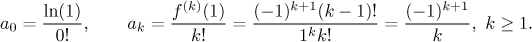
We had to (and will have to) treat the case
k = 0 separately, since
f (0) = f does not fit
the general pattern. The Taylor series is
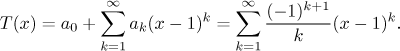
Now take any number x from the interval
(0,2).
We will use the
Lagrange
estimate of the remainder to prove that this Taylor series converges to
the logarithm at this x. If we denote by I the closed
interval with endpoints 1 and x, we have the estimate
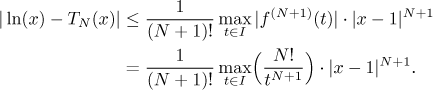
Now we need to ask where x is. If
x = 1, then
T(1) = 1 = ln(1). If
x > 1, then the interval I is
[1,x],
and since
1/tN+1
is a decreasing function, the maximum happens at 1.
Therefore
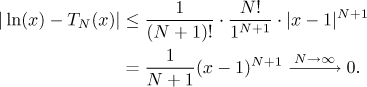
We used the fact that x < 2, therefore
(x − 1) < 1 and we know that
qN goes to zero if
|q| < 1
(see the
geometric
sequence).
So for x > 1 (and of course for
x < 2)
we have the convergence of
T(x)
to
ln(x)
proven.
When x < 1, then the interval I is
[x,1]
and the maximum of the decreasing function
1/tN+1
is attained at x.
Therefore
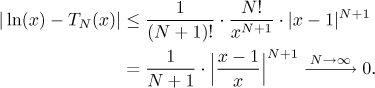
Now we have a little problem. If
x > 1/2, then the number in absolute value
is less than 1 and we get convergence using the good old geometric sequence
argument. On the other hand, for x
between 0 and 1/2 this argument fails, since the number in the
geometric sequence is larger than 1 and the upper Lagrange estimate goes to
infinity. However, note that it is only an upper estimate, so this does not
necessarily mean that the difference
|ln(x) − TN|
goes to infinity. Indeed it does not, we know that also there it actually goes to
zero, since in Theory - Series of functions -
Taylor series
we proved using a different method that the above Taylor series converges to
logarithm on (0,2].
This shows that on (0,1/2), the Lagrange estimate is too
generous.
![]()