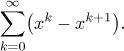
Here we will try to apply the standard tests to determine the convergence of the series

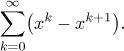
We treat x as parameter and sum up with respect to k. What tests can be used? Comparison seems out, since for k large we cannot really ignore anything. Actually, the expression k + 1 is pretty much like k for large values of k, but this is happening in the exponent of a power and thus we cannot use this simplification, since we know that it only works in fractions. Indeed, if we do try to use it, we get

This would suggest that this series converges for all values of x, which is obviously wrong, see below.

So comparison is out, how about the popular twins, Ratio and Root? We start with the Root test.

We see that the given series converges absolutely on the interval (−1,1). We can reach the same conclusion using the Ratio test.

We also know that for |x| > 1 our series diverges, here we use the version of the Root test for general series, see e.g. the note at the end of the section Root and Ratio tests in Theory - Testing convergence.

One can also show this directly. First we rewrite the terms of our series like this:

|a_k| = |x|^k⋅|1 − x|.

Now we see that for |x| > 1 the terms |a_k| go to infinity, therefore a_k do not go to zero.

It remains to individually check on the points x = −1 and x = 1, but we already did that.