Řešíme rovnice a nerovnice

V této sekci stručně připomeneme základní metody používané při řešení rovnic a nerovnic. Soutředíme se na prolémy, které mohou nastat, pro čtenáře může být překvapením, že se v této sekci použijí vlastnosti funkcí. Tato sekce má části Rovnice, Nerovnice, Znaménkové nerovnice, Dvojité nerovnice, Rozdělujeme reálnou osu a (Ne)rovnice s goniometrickými funkcemi.

Uvažujme rovnici, ve které vystupuje neznámá x. Obvyklá metoda řešení rovnic je osamostatnit x na jedné straně. Obecně postupujeme tak, že na obě strany rovnice aplikujeme operace, což funguje často, ale někdy je potřeba být opatrný, což je právě téma této části. Každý ví, že k obou stranám rovnice je možné přičíst či od nich odečíst cokoliv, ale při násobení a dělení rovnice je na místě opatrnost, protože to funguje pouze tehdy, když při násobení/dělení nepoužijeme nulu.

Co už dobře nezná každý je další trik, který se často používá. V mnoha rovnicích máme funkci, které se potřebujeme zbavit, například v rovnici ln(x) = 2. Nejjednodušší způsob je aplikovat (na obě strany) inverzní funkci k té, které se chceme zbavit, tato funkce a její inverze se pak navzájem zkrátí. Inverzní funkce k logaritmu je exponenciála, takže uděláme

e^ln(x) = e²,
x = e².

Ne vždy je to ovšem takto snadné. Podívejme se na následující dva příklady.

Příklad: Uvažujme rovnici arcsin(x) = π/2. Aplikujeme inverzní funkci.

sin[arcsin(x)] = sin[π/2],
x = 1.

Teď uvažujme tuto rovnici: sin(x) = 1. Pokud použijeme obdobný postup,

arcsin[sin(x)] = arcsin[1],
x = π/2,

dostaneme chybnou odpověď. Jak je to možné? Jaká je tedy správná odpověď?

Základem tohoto triku je pojem inverzní funkce. V prvním příkladě je sinus inverzní funkce k arkus sinu na intervalu ⟨−1,1⟩. Je x opravdu z tohoto intervalu? V tomto případě ano, protože arcsin neakceptuje žádné jiné hodnoty, tudíž už zadaná rovnice v sobě nese příslušné omezení pro x. Pracujeme tedy s arcsinem na oblasti, kde je invertibilní, a vzorec funguje.

Na druhou stranu arcsin není inverze k sinu, ale jen k sinu omezenému na interval . Zde už ale nemáme zaručeno, že x v rovnici je z této oblasti, a pro x z jiných oblastí máme jiné inverzní funkce. Nalezení řešení je proto mnohem komplikovanější a ve skutečnosti je jich nekonečně mnoho, jsou tvaru π/2+2kπ, kde k je libovolné celé číslo.

Podobný problém máme s odmocninami. Jedním směrem dostaneme všechna řešení:

 = 3,
[]² = 3²,
x = 9.

Fungovalo to, protože druhá mocnina je inverzní funkce k druhé odmocnině na intervalu ⟨0,∞) a žádné jiné x nejsou v dané rovnici možné. Opačné pořadí nefunguje.

x² = 16,
[x²]^1/2 = 16^1/2,
x = 4.

Problém je zase v tom, že abychom dostali inverzi k druhé mocnině, museli jsme ji omezit na ⟨0,∞), teď ale nemáme žádnou záruku, že to x v rovnici je z této oblasti. Správná odpověď je zde −4 a 4.

Zatím jsme měli problémy s chybějícími řešeními. Je také možné dostat falešná řešení. To je vlastně také spojeno s problémem inverze. Změníme rovnici a najdeme řešení té nové, ale jak víme, že je to také řešení původní rovnice? Je to pravda, pokud se můžeme vrátit od poslední k první (dané) verzi rovnice. Operace, které děláme, by tedy také měly fungovat v opačném směru. Jinými slovy, pokud máme dvě funkce, které jsou navzájem inverzními jen někde, pak máme jedním směrem problém a to se objeví buď cestou k řešení, nebo nás to kousne při zpětném chodu. Podívejme se na tento příklad.

(2-x²)^1/2 = x,
[(2-x²)^1/2]² = x²,
2-x² = x²,
2x² = 2,
x² = 1,
x = 1, −1.

Zdá se, že máme dvě řešení, ale funguje jen jedno, jmenovitě x = 1. Poznamenejme, že takovéto problémy se neobjevují při práci s logaritmem a exponenciálou, v pohodě jsou také třetí odmocnina a třetí mocnina a každý jiný pár navzájem inverzních funkcí, které nevyžadují restrikci. V ostatních případech musíme být velmi opatrní, hlavně je vždy potřeba ověřit zkouškou, že řešení, která jsme obdrželi, opravdu splňují danou rovnici v původním tvaru.

Pro zvládnutí takovýchto problémů není žádná univerzální metoda. U populárních funkcí víme, co se děje, například si pamatujeme, že odmocnina z x² není x ale |x|. Někdy, v případě kdy inverzní funkce existuje jen na částech reálné osy, pomůže rozdělit oblast, kde řešíme, na odpovídající části, viz příslušné téma níže.

S nerovnicemi můžeme mít všechny problémy, o kterým jsme mluvili výše, a ještě nějaké navíc. Zase můžeme přičíst/odečíst u obou stran a všichni víme, že když nerovnici násobíme/dělíme, tak musíme zjistit, jaké je znaménko čísla, kterým násobíme/dělíme. Pokud je toto číslo kladné, pak směr nerovnosti zachováme, ale když je záporné, musíme směr otočit. Pokud tento člen zahrnuje neznámou, pak znaménko vlastně neznáme a musíme nerovnici řešit několikrát, abychom pokryli všechny možné situace, viz část Rozdělujeme reálnou osu.

Když aplikujeme funkci na nerovnici, máme dva zádrhele. První je s krácením inverzních funkcí, což způsobuje problémy podobně těm předtím. Zde ale musíme být opatrní už při aplikaci funkce na nerovnice, protože ne každou funkci na ně můžeme aplikovat. Podmínka je jednoduchá. Aplikovat můžeme jen funkce, které jsou monotonní; pokud je funkce rostoucí, tak necháme nerovnost tak, jak byla; pokud je funkce klesající, pak musíme u nerovnosti změnit směr. A zase někdy máme funkci, která je monotonní jen někde a pak je to teprve zajímavé.

Například logaritmus a exponenciála jsou funkce rostoucí všude. Proto můžeme vyřešit nerovnici e^x < 5 aplikováním logaritmu na obě strany beze změny směru, dostaneme ln(e^x) < ln(5), tedy x < ln(5). Naopak x² není monotonní, takže obecně nemůžeme umocňovat obě strany nerovnice na druhou, to lze jen ve specálních případech (například pokud nějak víme, že jsou obě strany kladné, protože na kladné poloose je druhá mocnina rostoucí).

Pro populární funkce máme triky na řešení nerovnic. Pokud jsou do toho zapleteny polynomy, můžeme použít přístup přes grafy nebo trik popsaný v části Znaménkové nerovnice. Obrázky pomohou také při práci s goniometrickými funkcemi, další přístup ukážeme v poslední části této sekce.

Znaménkovými nerovnicemi myslíme nerovnice, kde jedna strana je 0, pak u výrazu na druhé straně není důležitá přesná hodnota, ale jen znaménko. Tyto nerovnosti lze řešit docela snadno, pokud tu druhou stranu dokážeme vyjádřit jako součin či podíl jednoduchých členů, protože znaménko takového výrazu určíme snadno ze znamének jednotlivých faktorů. Stačí tedy zkoumat znaménka jednotlivých faktorů a pak to nějak dát dohromady.

Při troše štěstí je každý z těchto jednoduchých výrazů spojitý a jako takový mění znaménka způsobem, který se dá dobře hlídat. Přesně řečeno, reálná osa se rozpadne na několik oblastí, na každé z nich už má tento výraz jen jedno znaménko a dělící body (kde se znaménka mění) jsou přesně ty body, kde je tento výraz roven nule. Protože v každé jednotlivé oblasti je znaménko všude stejné, určíme jej jednoduše tak, že si odtud vybereme nějaký bod a dosadíme.

Například x² − 1 je nula v −1 a v 1, takže se reálná osa rozdělí na oblasti (−∞,−1), (−1,1) a (1,∞). Z prvního vybereme například x = −2, dosadíme a dostaneme 3 > 0, takže x² − 1 je na první oblasti kladné, podobně zjistíme, že tento výraz je záporný na druhé a kladný na třetí oblasti.

Z toho dostaneme postup pro řešení znaménkových nerovností.

Nejprve najdeme nulové body všech faktorů. Pak je použijeme, abychom rozdělili reálnou osu na oblasti. Pro každou oblast najdeme znaménka všech faktorů. To uděláme tak, že z jejího vnitřku vybereme nějaký bod a dosadíme do všech faktorů. Pak v každé oblasti dáme znaménka faktorů dohromady pomocí znaménkové algebry a dostanem znaménko celého výrazu. V posledním kroku shromáždíme všechny oblasti, kde znaménko splňuje danou nerovnici. Pokud je nerovnost ostrá, použijeme otevřené intervaly. Pokud zahrnuje i rovnost, pak přidáme koncové body, ale jen pokud ve výrazu nepůsobí problémy.

Pro lineární faktory je to dokonce ještě snažší, protože lineární faktory mění znaménko jen jednou, v bodě, kde jsou nulové, takže pro konkrétní lineární faktor si označíme bod, kde je nula, a pak je to jedno znaménko všude doprava a druhé doleva. Abychom zjistili, které je které (zda to jde − + nebo + −), prostě jen dosadíme libovolné číslo jiné než nulový bod.

Někdy nedělíme celou reálnou osu, ale jen její část, to když jsou některá čísla zakázaná nějakými výrazy v nerovnosti. Nestává se to často (většinou pracujeme jen s polynomy), ale když už se to stane, tak to není problém, jak uvidíte v následujícím příkladě.

Příklad: Uvažujme nerovnici

Máme tu jeden problém, logaritmus akceptuje pouze kladná čísla. Příslušná nerovnost je x + 2 > 0, takže už od začátku své výpočty omezíme na x > −2. Teď začneme obvyklý algoritmus. Nejprve nulové body. Rovnice 3 − x = 0, x + 5 = 0, x − 1 = 0, 2x − 1 = 0, ln(x + 2) = 0 mají řešení x = 3, x = −5, x = 1, x = 1/2 a x + 2 = 1, tj. x = −1.

Tyto body uspořádáme dle velikosti a pak se podíváme, jak rozdělí oblast (−2,∞), kde pracujeme; například vidíme, že x = −5 tam nespadá a je tudíž irelevantní. Dostaneme oblasti (−2,−1), (−1,1/2), (1/2,1), (1,3) a (3,∞). K určení znamének v těchto oblastech použijeme tabulku.

Chceme, aby výraz byl kladný, takže ty pravé oblasti jsou (−2,−1), (1/2,1) a (1,3). Protože i nula je nerovnicí povolena, podíváme se, které koncové body těchto tří intervalů nepůsobí problémy. Vidíme, že −2 je mimo kvůli logaritmu, 1/2 a 1 dávají nulu ve jmenovateli, takže jediný fungující bod je 3. Odpověď je

(−2,−1) ∪ (1/2,1) ∪ (1,3⟩.

Všimněte si, že tuto nerovnici také můžeme vyřešit tím, že se nejprve zbavíme zlomku, což znamená, že bychom museli vynásobit obě strany jmenovatelem. Na to bychom ale museli zkoumat možná znaménka jmenovatele, následně bychom museli rozdělit reálnou osu a řešit několik nerovnic (viz část Rozdělujeme reálnou osu), nejspíše by to bylo mnohem horší než toto řešení. Určování znamének je obvykle nejrychlejší řešení. Proto také často transformujeme i jiné nerovnice na tento typ, například takto.

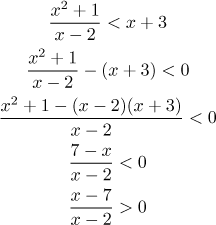
Dělící body jsou 2 a 7, vidíme, že řešení je (−∞,2) ∪ (7,∞).

Dvojité nerovnice vypadají jako tyto dva příklady.

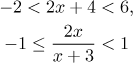
Jsou obvykle dva způsoby, jak takové dvojité nerovnice řešit. Jeden je řešit obě najednou tak, že aplikujeme operace na všechny tři strany. To je někdy velice snadné, například u toho prvního příkladu.

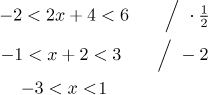
Řešením je interval (−3,1). Druhý příklad už ale nevypadá tak dobře. První krok by bylo vynásobit všechny strany jmenovatelem x + 3, ale protože neznáme jeho znaménko, museli bychom rozdělit reálnou osu a řešit celý problém dvakrát. Ukážeme to v části Rozdělujeme reálnou osu níže, uvidíte, že je to tak delší.

Druhá možnost je prostě vyřešit každou nerovnici zvlášť a pak proniknout obě řešení (chceme, aby platily obě nerovnice). To je často snažší, zvlášť pokud umíme změnit obě rovnice na znaménkové. Pro druhý příklad by tohle byla moje volba metody. Připomeňme, že "obrácené vé" značí logickou spojku "a".

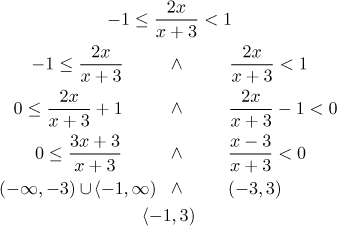
Často jsme v situaci, kdy řešíme (ne)rovnici, ale krok, který chceme udělat, vyžaduje určitou znalost, kterou nemáme, jmenovitě znaménko nějakého výrazu. Dva nejpopulárnější důvody pro toto jsou, že chceme nerovnost násobit/dělit určitým výrazem nebo že se chceme zbavit absolutní hodnoty.

Pokud tento výraz zahrnuje proměnnou x, pak neznáme jeho znaménko. Pak potřebujeme prozkoumat situaci pro obě možnosti pro znaménko, ale každé z těchto řešení bude fungovat jen na části reálné osy, jmenovitě tam, kde má onen výraz to či ono konkrétní znaménko. Proto tedy rozdělíme reálnou osu podle toho, které znaménko kde máme, a vyřešíme problém v každé části zvlášť, nakonec vezmeme sjednocení všech částečných řešení. Připomeňme ale, že výsledky získané během řešení v jedné konkrétní oblasti platí pouze v rámci této oblasti, tj. všechny části, které jsou mimo tuto oblast, musí být ignorovány (jinými slovy, řešení, které dostaneme v této konkrétní oblasti, musí být s touto oblastí proniknuto, než jej použijeme dále).

Pro příklad se vrátíme k druhé dvojité nerovnosti výše. Rádi bychom celou tu věc pronásobili členem x + 3, ale na to potřebujeme znát jeho znaménko, ať víme, zda není třeba změnit směr v nerovnosti. Jsou dvě možnosti a musíme obě vyzkoušet. Vidíme, že ten výraz je kladný pro x > −3 a záporný pro x < −3, což určuje oblasti, na které rozdělíme reálnou osu. Pak v každé z nich problém vyřešíme.

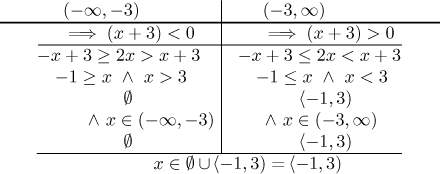
Pokud máme více obtížných členů, tak si zjistíme všechny jejich dělící body a uděláme univerzální rozdělení reálné osy, takže na každé oblasti už jsou všechny určeny.

Příklad: Uvažujme dvojitou nerovnost

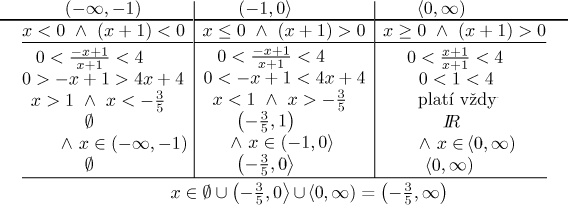
Všimněte si zase, jak jsme v každé oblasti protínali řešení, které jsme v ní získali, s touto oblastí, na konci jsme je všechna spojili sjednocením.

Zde ukážeme jen jeden užitečný trik. Počátečním bodem budou jednoduché (ne)rovnice typu sin(x) = 1 či cos(x) < 1/2. Nejednodušší způsob, jak takové (ne)rovnice řešit, je použít příslušný graf. Asi nejsnadnější je nejprve identifikovat řešení v rámci jedné periody a pak k němu přidat periodicitu.

Pro první rovnost bychom nejprve usoudili, že na první periodě sinu máme řešení x = π/2, pak přidáme periodicitu: x = π/2 + 2kπ.

U druhého příkladu to funguje podobně. Z obrázku vidíme, že se řešení dá popsat nerovnostmi π/3 < x < 4π/3, pak přidáme periodicitu:

π/3 + 2kπ < x < 4π/3 + 2kπ.

Co uděláme, když je argument goniometrické funkce nějak transformován? Uvažujme nerovnici cos(2x + 1) < 1/2. Jak ji vyřešíme? Jsou dvě populární metody.

Jedna je přímé použití obrázku, ale tentokrát je třeba nakreslit graf funkce cos(2x + 1). To by neměl být problém pro zkušeného studenta (viz Transformace a odhad grafu v části Funkce - Přehled metod - Základní vlastnosti reálných funkcí). Může to ale být zrádné, takže někteří lidé (například já) dávají přednost druhému způsobu.

Ona druhá metoda používá normální graf příslušné goniometrické funkce a nejprve předstíráme, že je v argumentu jen x. Najdeme řešení přesně tak, jako předtím, ale pak namísto x dosadíme argument a vyřešíme pro x. V našem příkladě by to šlo takto:

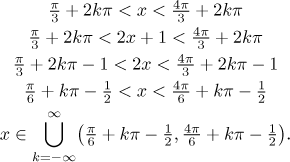
Odpověď jsme vyjádřili množinovým popisem, jmenovitě pomocí nekonečného sjednocení, ale jak vidíte, jakmile máme řešení popsáno nerovnostmi, je pak už snadné přejít k intervalům. Výhoda této metody je, že ji můžeme použít i pro obecnější transformace, které by se špatně kreslily, například při řešení nerovností jako je tato: 0 ≤ tg(x²+1) < 1.