Funkce více proměnných: Úvod

Funkce více proměnných jsou přirozeným zobecněním funkcí jedné proměnné. Funkce jedné proměnné je zobrazení (jakési posílátko) z jedné kopie reálných čísel (typicky její podmnožiny) do druhé. Funkci více proměnných dostaneme, když výchozí jednorozměrnou množinu nahradíme množinou vícerozměrnou.

Lidé si obvykle s pojmem funkce spojují vzorec (což není vždy možné, ale typicky to tak potkáváme), i pak je funkce více proměnným zcela logickým krokem od vzorců jako f (x) = x² ke vzorcům jako f (w,x, y,z) = (e^w + y)^x⋅sin(x − πz). Značení jako f (x, y), f (x, y,z) či f (u,v,w,x, y) je velice pohodlné pro práci s konkrétními funkcemi, kdy víme, kolik je proměnných, ale nehodí se pro obecné úvahy, kdy pracujeme s neznámým počtem proměnných. V takovém případě se vyplatí vidět situaci tak, že pořád máme jednu proměnnou, jen se tentokráte bere z množiny vektorů. Pak prostě píšeme f ().

V tomto značení je pak také práce s funkcemi více proměnných v mnohém obdobná práci s jednou proměnnou, hlavní myšlenky zůstávají, jen výpočty a postupy jsou občas komplikovanější. Vše se ale zvládá výrazně snáze, pokud si to člověk umí propojit s geometrickou představivostí, zde se hodí zkušenost se základními objekty ve vícedimenzionálním prostoru (přímky, roviny atd.)

To je také hlavním cílem těchto kapitolek, ukázat na geometrický význam pojmů, výpočtů a postupů. Nejprve si dáme definici funkce více proměnných, ať víme, s čím budeme pracovat.

Definice.
Funkcí více proměnných rozumíme libovolné zobrazení f : D ↦ ℝ, kde D = D( f ) je nějaká podmnožina ℝⁿ.

Není-li D explicitně dáno, pak jako definiční obor D( f ) bereme množinu všech ∈ℝⁿ, pro kterou má f () smysl.

Definiční obor

U funkcí zadaných vzorcem se definiční obor hledá obdobně jako u funkce jedné proměnné, tedy položíme si otázku, jaká omezení na proměnné vyplývají z onoho daného vzorce.

Na rozdíl od případu jedné proměnné se nemusíme snažit vyjádřit výslednou množinu v nějakém standardizovaném tvaru (sjednocení intervalů), protože to ve více rozměrech prostě nelze, množiny jsou příliš rozmanité na to, aby se daly zapsat pomocí jednoho základního typu (či několika typů). Ušetříme tedy práci, stačí výsledek napsat ve tvaru

D( f ) = {∈ℝⁿ; podmínky pro }.

Naopak nová věc nemající smysl v jedné dimenzi je, že u množin ve vícerozměrném prostoru někdy můžeme rozeznat, jaký je to vlastně objekt.

Příklad
Určíme D( f ) těchto funkcí:

a) f (x, y) = x ²sin(x + y):     evidentně D( f ) = ℝ².

b) :     D( f ) = {(x, y)∈ℝ²;  x² + y² ≤ 3²},
je to kruh se středem v počátku o poloměru 3.

c) :     D( f ) = {(x, y,z)∈ℝ³;  x² + y² + z² ≤ 3²},
je to koule se středem v počátku o poloměru 3.

d) 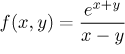:     D( f ) = {(x, y)∈ℝ²;  y ≠ x},
je to rovina s vynechanou přímkou---hlavní diagonálou (viz obrázek níže).

e) :     D( f )={(x, y)∈ℝ²;  y⋅x ≥ 0},
je to uzavřený první a třetí kvadrant v rovině.

Vizualizace funkcí (náčrt grafu)

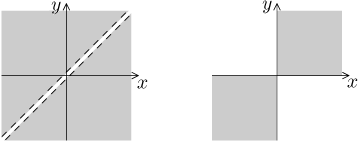
Funkce jedné proměnné si nejčastěji vizualizujeme pomocí grafu. Zobecnění na více proměnných je vcelku snadné. V jedné proměnné je grafem funkce podmnožina dvourozměrného prostoru daná jako souhrn všech bodů ve tvaru (x, f (x)) pro x∈D( f ). Pokud se proměnná funkce  f () bere odněkud z prostoru ℝⁿ, pak na graf budeme potřebovat o jednu dimenzi víc a vznikne jako množina bodů ve tvaru (x₁,x₂,...,x_n, f ())∈ℝⁿ⁺¹,  = (x₁,...,x_n).

V případě n ≥ 2 tedy potřebujeme alespoň tři dimenze, čímž vyskočíme z papíru a hned vidíme, že graf vlastně nelze nakreslit. Přesto je dobré si zachovat alespoň ideovou představu grafu. Na "vodorovné" reprezentaci definičního oboru (přesné či symbolické) najdeme výchozí hodnotu vícerozměrné proměnné, nad ní zakreslíme bod grafu ve výšce odpovídající funkční hodnotě v daném bodě.

Pokud to uděláme ve všech bodech definičního oboru, body grafu vytvoří jakýsi útvar, který si můžeme představit jako zvlněný povrch. V zásadě takto to bude fungovat v případě dvou proměnných, typickým grafem je nějaký plochý (v principu dvourozměrný) objekt coby součást třírozměrného prostoru, při troše štěstí si jej dokážeme vhodným stínováním a podobně alespoň přiblížit. Například grafem konstantní funkce f (x,y) = c bude vodorovná rovina vznášející se nad základními osami x,y v patřičné výšce c.

S funkcemi dvou proměnných pracujeme rádi právě proto, že si je obvykle umíme načrtnout. Zkušenost by měla naznačit, že jsou i funkce dvou proměnných, u kterých to tak pěkné nebude, grafem je obecně nějaká množina v ℝ³, která může být i velmi divoká, ale takové funkce nejspíše v běžných aplikacích nepotkáme.

Pokud máme tři a více proměnných, tak už si graf neznázorníme ani přibližně, čtyřrozměrný prostor je nad naši představivost. Proto se hledaly jiné způsoby, jak si chování funkcí více proměnných vizuálně přiblížit. Zde si ukážeme ty nejpoužívanější.

Tyto metody jsou užitečné i pro případ n = 2, protože nám pomáhají odvodit, jak takové grafy opravdu vypadají, a zhotovit věrný náčrt. Protože grafy funkcí dvou proměnných umíme opravdu nakreslit, uvidíme přímo, jak ty metody vlastně fungují. Získáme tak jakýsi náhled do nových pojmů, který se doufejme přenese i do vyšších dimenzí, kde už si to opravdu představit nedokážeme.

Kromě těchto metod je možné náčrt grafu funkce dvou proměnných získat také pomocí rozličných programových prostředků (Maple, Mathematica atd.), což je pohodlné a příjemné, nicméně je dobré věcem rozumět, ostatně občas tyto výpočetní prostředky selhávají a zůstává starý dobrý mozek a znalosti.

Hladiny konstantnosti.

Toto je jedna z nejsilnějších metod pro vizualizaci chování funkce, ale tento pojem se dá využít i šířeji, například ke zkoumání implicitně zadaných útvarů.

Definice.
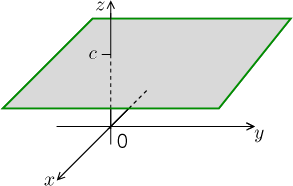
Nechť f: D( f ) ↦ ℝ je funkce, kde D( f ) ⊆ ℝⁿ. Pro c∈ℝ definujeme příslušnou hladinu konstantnosti

H_c = {∈D( f );  f () = c}.

Jak to funguje? Nejprve graf řízneme na úrovni c (zeptáme se, kde všude jsou hodnoty funkce rovny c) a pak se podíváme, ze kterých hodnot proměnných se tam dostaneme, neboli si tento řez promítneme do definičního oboru. Pokud si graf představíme jako reliéf krajiny, tak hladina konstantnosti jsou místa daná pomocí zeměpisných souřadnic (tedy v rovině mapy) taková, že je v nich nadmořská výška přesně c. Jinými slovy, hladiny konstantnosti jsou analogické vrstevnicím na mapě. Zkušený turista dokáže z vrstevnic odhadnout tvarování krajiny, stejně tak lze z hladin konstantnosti odhadnout mnoho užitečného o dané funkci.

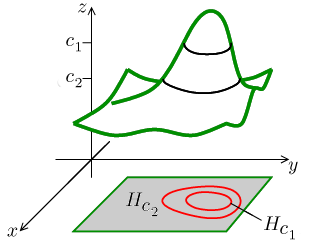
Z definice vidíme, že H_c leží v D( f ), takže na znázornění hladin nám stačí jen n rozměrů, což je pokrok oproti grafům. Je to jeden z užitečných způsobů, jak analyzovat funkce tří proměnných. Pokud máme například funkci T(x,y,z) popisující teplotu v různých místech jisté místnosti, pak pro rozličné volby teploty c dostáváme příslušné hladiny konstantnosti H_c jako jakési "obláčky" ukazující, kde v místnosti je zrovna dotyčná teplota. Tyto obláčky jsou třírozměrné, je tedy možné si je pomocí perspektivy znázornit ve 2D (na papíře). Při porovnání těchto nákresů pro různé hodnoty c získáme velice dobrou představu o chování teploty, je také možné tyto nákresy spojit do animace a podobně. Obrázek níže ukazuje, jak by také mohly vypadat dva teplotní "snímky" učebny v únoru, kdy ji vytápějí tři studenti potící se u zkoušek.

Řezy.

Řezy jsou jednoduchým, ale velice užitečným nástrojem pro zkoumání vícerozměrných situací. Aby pro nás byly opravdu jednoduché, musíme jim dobře rozumět a vnímat vazbu mezi vzorci a geometrickou představou. Základní myšlenkou je, že si z mnoharozměrné situace vyřízneme pomocí roviny dvourozměrný "průřez", který již umíme (doufejme) prozkoumat pomocí nástrojů pro zkoumání (grafu) funkce jedné proměnné.

Vyjdeme tedy ze situace, kdy se proměnné berou ze světa ℝⁿ, který si v obrázku symbolicky představíme jako vodorovný útvar. Vybereme si nějaký počáteční bod a uvažujeme přímku p v ℝⁿ procházející tímto bodem ve směru . Body této přímky jsou dány (pokud se pohybujeme rovnoměrně) parametrickou rovnicí  =  + t, můžeme si představit, že je to popis cesty, kterou vykonáváme v definičním oboru D( f ). V čase t jsme v jistém bodě z D( f ) a tomu odpovídá hodnota funkce f (+t). Vzniklo zobrazení t ↦ f (+t), které popisuje tvar grafu, který nad sebou "vidíme" při pohybu po přímce p. Přímka p tedy určila řez, který získáme jako průnik grafu f a "svislé" roviny vztyčené nad p.

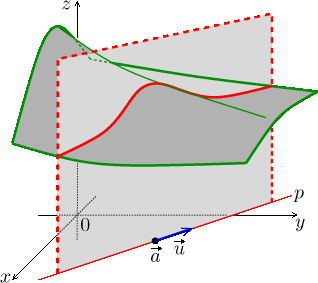
Tento řez má tvar, jenž zjevně souvisí s funkcí φ(t) = f (+t), která má jen jednu proměnnou a umíme ji hravě vyšetřit. Bohužel tato souvislost není tak jednoduchá, jak bychom doufali, tedy že když si nakreslíme graf funkce φ(t), tak rovnou uvidíme tvar řezu. Problém je v měřítku, na našem dvourozměrném obrázku řezu bude značka pro "1" (pozice v čase t = 1) v místě  + , což ovšem nemusí být ve vzdálenosti 1 od bodu v původním mnoharozměrném obrázku grafu f. Míra zkreslení evidentně závisí na velikosti směrového vektoru , což by nemělo překvapit: Čím rychleji jedeme, tím více se nám subjektivně zkreslí krajina kolem ("zmáčkne se", míjíme věci rychleji). Proto se vždy snažíme pracovat se směrovými vektory velikosti jedna (pokud nám v tom nějak nezabrání například praktická aplikace, se kterou pracujeme), pak nám bude geometrická informace souhlasit. Na tyto souvislosti znovu narazíme v kapitole o derivacích.

Příklad
Uvažujme funkci

Podíváme se, jak vypadá řez jejím grafem svislou rovinou nad přímkou (x,y) = (2,3) + t(−1,1). Interpretace: Funkce f dává nadmořskou výšku, my stojíme na místě s GPS souřadnicemi (2,3) a vydáme se směrem (−1,1), přitom nás zajímá, jakým způsobem stoupáme a klesáme.

Předpis pro přímku nám dává x = 2 − t, y = 3 + t, po dosazení do funkce f dostáváme pomocnou funkci

Poslední vzorec ukazuje, že graf funkce φ má tvar kopečku, jehož vrchol je v čase t = 1. Není to přesná podoba řezu grafem funkce f, protože |||| = ||(−1,1)|| je rovno odmocnině ze dvou, není to jednotkový vektor. Skutečný tvar řezu je tedy oproti grafu funkce φ trochu "zmáčknut" ve vodorovném směru, to ale nemění jeho hlavní podobu. Můžeme tedy konstatovat, že odpovídající řez grafem funkce f má tvar kopečku, jehož nejvyšší vrchol je v bodě odpovídajícím času t = 1, tedy v bodě (1,4).

Podotkněme, že to ještě nemusí znamenat, že graf funkce f jako takový tam má kopeček. Pro příklad takové situace se můžeme podívat na obrázek výše, který sice nemá úplně správný tvar grafu f, ale situaci vystihuje, řežeme skrz úbočí a dostali jsme kopec. Obrázek má dokonce na správném místě bod , vektor a přímku p, i tvar řezu je v zásadě v pořádku.

Poznamenejme, že pokud bychom chtěli dostat přesný tvar řezu, popřípadě chtěli s tímto řezem dále pracovat analyticky a geometricky, tak bychom museli uvažovat směrový vektor

Výpočty jsou pak obdobné, jen drobet méně příjemné.

Nejčastěji používáme přímky rovnoběžné s osami, protože dostáváme dobře zpracovatelné výstupy, graficky i analyticky (vidíme vliv jednotlivých proměnných). Například pokud jsme v ℝ³ v bodě (x₀, y₀,z₀) a chceme se pohybovat ve směru osy y, dostáváme přímku t ↦ (x₀, y₀ + tu,z₀). Jinými slovy, proměnné, které nás nezajímají, necháme konstantní a měníme pouze jednu. To je intuitivně velice snadný proces. Vzhledem k tomu, že preferujeme směrový vektor o velikosti 1, používáme standardně příjemné přímky ve tvaru t ↦ (x₀ + t, y₀,z₀), t ↦ (x₀, y₀ + t,z₀) atd. Znamená to tedy, že zafixujeme hodnoty většiny proměnných a jednu necháváme měnit běžným způsobem, což se odráží i v zápisu: Nepotřebujeme zavádět t a jen zkoumáme přímky jako x ↦ (x, y₀,z₀), y ↦ (x₀, y,z₀) atd.

Tento pohled se dá zobecnit tak, že si zafixujeme určitý počet proměnných a hýbeme s ostatními, čímž si snižujeme počet dimenzí, se kterými pracujeme, podle toho, co nás zrovna zajímá. Představme si na chvíli funkci T(x, y,z) tří proměnných, například popisující teplotu v různých místech v přednáškárně, a určitý bod  = (x₀, y₀,z₀).

Pokud si zafixujeme hodnoty y = y₀ a z = z₀, dostáváme jednorozměrný objekt neboli přímku, kdy se z bodu pohybujeme jen ve směru osy x a sledujeme teploty. Jde o jednorozměrnou situaci x ↦ T(x, y₀,z₀), kterou snadno prozkoumáme a znázorníme.

Pokud si zafixujeme pouze proměnnou z = z₀, pak máme dva stupně volnosti, pohybujeme se tedy na (vodorovné) rovině procházející bodem , která je kolmá na osu z. Vzniká tedy funkce dvou proměnných (x, y) ↦ T(x, y,z₀), jejíž graf si pořád ještě dokážeme při troše štěstí přiblížit v perspektivě (třeba stínováním).

Dostáváme tak další nástroj ke zkoumání funkcí. Nejčastěji ovšem pracujeme právě s pohybem po přímce a jednorozměrnou situací.

Standardní tvary.

V případě funkce jedné proměnné často nahlížíme na graf jako na analytický objekt v rovině daný rovnicí y = f (x), mnohé z těchto objektů umíme poznat. Například graf funkce f (x) = 1 − 2x je útvar popsaný rovnicí y = 1 − 2x neboli 2x + y = 1 a my víme, že jde o přímku. Toto často výtečně funguje i v případě více proměnných.

U funkcí n proměnných dostáváme objekt v ℝⁿ⁺¹ daný rovicí y = f (). I zde lze doufat, že takový útvar poznáme, například funkce f (x, y) = 2x + y − 5 vede na rovnici 2x + y − z = 5, což definuje rovinu v ℝ³.

Někdy si vzniklou rovnici musíme upravit, pak ale musíme dát pozor, že tím může vzniknout větší množina. Na to už jsme ostatně museli dávat pozor i u funkcí jedné proměnné. Víme například, jak vypadá tvar grafu funkce f (x) = . Pokud si rovnici y =  přepíšeme jako x = y², hned rozpoznáme parabolu, jen má prohozené role proměnných, tudíž to bude parabola, která jde směrem vpravo, nad a pod osou x. Graf funkce f (x) =  je ovšem jen horní polovina tohoto útvaru.

Takové zvětšení (nebo zmenšení) množiny nastává, pokud při změně rovnice provedeme neekvivalentní úpravu, což je například ono umocnění. Zkušenost napoví, kdy je třeba dát si pozor.

Aby mělo rozpoznávání tvarů úspěch, musíme znát základní geometrické objekty. Jde zejména o ploché útvary (přímky, roviny) a útvary s kvadratickými rovnicemi, což je ve dvou rozměrech známá rodinka kuželoseček (parabola, kružnice a obecněji elipsa, hyperbola), ve více rozměrech se to dá zkombinovat bohatěji. Je samozřejmě jasné, že by člověk musel mít opravdu velké štěstí, aby se při výběru z nekonečně mnoha možných funkcí trefil zrovna do jedné z těch pár rovnic, které zná, ale ono to nastává častěji, než by se čistě na základě pravděpodobnosti dalo čekat, a když to vyjde, tak to velmi potěší.

Příklad.
Zde si ukážeme jednotlivé metody na funkci

Definiční obor: D( f ) = {(x, y)∈ℝ;  x² + y² ≤ 3²}.
Je to kruh o poloměru 3 se středem (0,0). Graf tedy bude nad ním, viz f (x, y) ≥ 0.

Začneme hladinami konstantnosti. Vidíme hned z definice funkce, že její hodnoty leží v rozmezí 0 až 3, odpovídající hladiny konstantnosti tedy budou zajímavé, ostatní jsou prázdné. Jak pro c∈⟨0,3⟩ hladina konstantnosti H_c vypadá?

Je to množina daná vztahem f (x, y) = c neboli x² + y² = 9 - c², toto specifikuje kružnici o poloměru ležící v definičním oboru. Pro větší hodnoty c (tedy větší hodnoty funkce) jsou kružnice menší, blíže ke středu, a naopak, pro hodnotu c = 0 dostáváme jako hladinu konstantnosti přímo kružnici o poloměru 3, tedy hranici definičního oboru.

Závěr: Funkce je nulová na krajích definičního oboru, největší v jeho středu, tak vypadají kopečky. Na obrázku jsou hladiny konstantnosti červeně v definičním oboru, odpovídající úrovně hodnot jsme na grafu vyznačili čárkovaně.

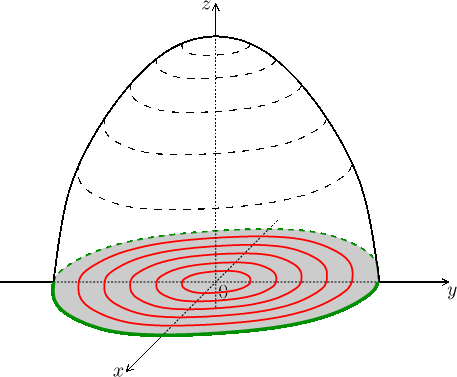
Protože jsou hladiny coby kružnice rotačně symetrické vůči středu, můžeme usoudit, že dotyčný graf je symetrický vzhledem k rotaci okolo osy z.

Nyní se podíváme na řezy. Zvolíme-li x = 0, pak se ptáme, jak vypadá graf nad osou y. Dostáváme

grafem je horní půlkružnice. Pro jiná pevně zvolená x = a jsou grafem menší půlkružnice

Takto tedy vypadají řezy svislými rovinami rovnoběžnými s osou y.

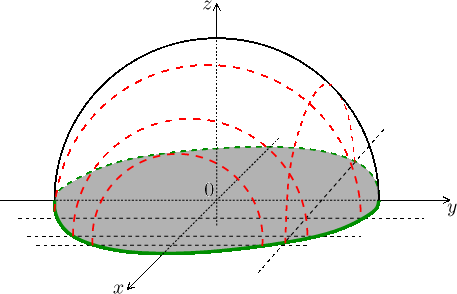
Funguje to i symetricky, takže také svislé řezy grafem rovnoběžné s osou x jsou horní půlkružnice. Nejde tedy patrně o kopeček ledajaký, ale o kopeček sférického tvaru.

Zkusíme to potvrdit rozpoznáním křivky. Graf f je dán rovnicí

což si hravě přepíšeme jako x² + y² + z² = 3² a dostáváme rovnici sféry. Graf funkce určitě nebude celá sféra (ta nabízí dvě různé hodnoty pro jeden bod (x, y)), ale nějaká její podmnožina. Protože D( f ) je kruh v rovině xy o poloměru 3, bude graf zabírat celou rozlohu oné sféry, a ze vztahu f (x, y) ≥ 0 vyplývá, že jde jmenovitě o její horní polovinu, což ostatně naznačily již hladiny konstantnosti a řezy.

Závěr: Graf funkce f je horní polosféra (dóm).

Příklad.
Teď se podíváme na funkci

f (x, y) = x² + y².

D( f ) = ℝ².

Hladiny konstantnosti: x² + y² = c, jsou to kružnice, jejichž poloměry se zvětšují se zvětšující se hodnotou funkce. Tedy čím dál jsme od středu, tím větší je funkce, to vypadá na jámu. Protože jsou všechny hladiny konstantnosti rotačně invariantní (po otočení okolo svislé osy vypadají pořád stejně), bude takový i graf.

Řezy: Zvolíme-li x = 0, dostáváme f (0, y) = y², grafem je parabola. Pro jiná x jsou grafem paraboly f (x₀, y) = x₀² + y² posunuté nahoru tím více, čím dále jsme od počátku, vrcholy těchto parabol jsou samy na parabole. Funguje to i symetricky.

Když k tomu přidáme pozorování o symetrii, závěr je jasný. Graf je rotační paraboloid.

Příklad.
Teď se podíváme na funkci

f (x, y) = x² − y².

D( f ) = ℝ².

Hladiny konstantnosti: x² − y² = c neboli hyperboly se zvětšujícím se poloměrem.

Řezy: Zvolíme-li x = 0, dostáváme f (0, y) = −y², grafem je parabola otočená dolů. Pro jiná x jsou grafem dolů otočené paraboly f (x₀, y) = x₀² − y² posunuté nahoru tím více, čím dále jsme od počátku, vrcholy těchto parabol jsou na parabole otočené vzhůru.

Zvolíme-li y = 0, dostáváme f (x,0) = x², grafem je parabola. Pro jiná y jsou grafem paraboly f (x, y₀) = x² − y₀² posunuté dolů tím více, čím dále jsme od počátku, vrcholy těchto parabol jsou na parabole otočené dolů.

Pomocné metody: Rotační symetrii nemáme, rovnice z = x² − y² také nepatří k nejznámějším. Nezbývá než si o tvaru udělat představu z řezů.

Závěr: Je to zvláštní graf, který stojí za nakreslení.

Funkce více proměnných: Derivace
Zpět na Extra - Funkce více proměnných