Funkce více proměnných: Derivace

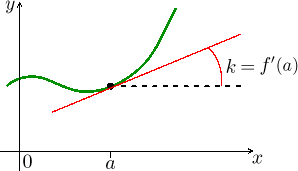
Nejprve si připomeňme hlavní významy derivace u funkce jedné proměnné. Je-li zvolena hodnota proměnné x = a, pak derivace f ′(a) udává směrnici tečny ke grafu f v odpovídajícím bodě. V aplikacích je pak zásadní další interpretace, hodnota f ′(a) udává, jak rychle se bude funkce f měnit (a graf růst či klesat), pokud procházíme proměnnou přes bod a (jednotkovou rychlostí).

Třetí užitečný pohled je, že derivace umožňuje aproximovat hodnoty funkce na okolí bodu a pomocí tečny, vzorec je (ve dvou podobách)

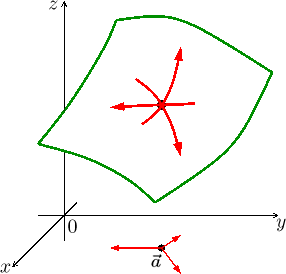
Žádná z těchto interpretací neobstojí u funkcí více proměnných. Je to jasné již z obrázku funkce dvou proměnných: Pokud zvolíme bod ∈D( f ) a stojíme v odpovídajícím místě na grafu, pak není vůbec jasné, co je to tečna. Odpověď je zjevná rovněž na otázku, jak rychle graf roste či klesá, pokud projdeme proměnnou přes : Záleží na tom, kudy půjdeme, protože na rozdíl od situace s jednou proměnnou teď máme úžasnou svobodu volby.

Touto úvahou jsme se nicméně dostali k jednomu z klíčových pojmů. Pokud nám někdo řekne, kterým směrem se z vydat, pak už má otázka na rychlost růstu grafu smysl.

Příklad.
Uvažujme funkci f (x, y) = x² + y², jsme v bodě  = (1,2). Co se stane, když se vydáme v určitém směru  = (h,k)?

Pohybujeme se na přímce dané parametrickou rovnicí (x, y) = (1,2) + t(h,k), přitom potkáváme funkční hodnoty

φ(t) = f (1 + th,2 + tk) = (1 + th)² + (2 + tk)² = (h² + k²)t² + (2h + 4k)t + 5.

Jde samozřejmě o situaci s řezem, kterou jsme již viděli v úvodní části. Graf funkce f jsme proťali svislou rovinou nad přímkou danou vzorcem t ↦  + t a očekáváme, že dostaneme snadno zvládnutelnou dvourozměrnou situaci.

Opravdu jsme dostali funkci φ jedné proměnné, můžeme ji tedy zderivovat a hodnota derivace v čase t = 0 nám řekne, jak rychle se hodnota funkce mění, když procházíme bodem .

Geometricky, graf funkce f jsme řízli svislou rovinou a tento řez pak představuje jednorozměrnou situaci, kde již derivaci spočítáme snadno.

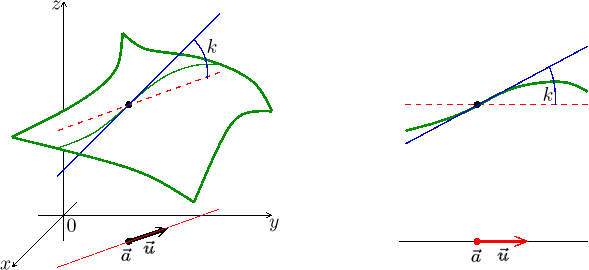
Pokud se například vydáme z bodu ve směru  = (−1,1), tak nám výsledek derivování odpovídající funkce φ(t) = 2t² + 2t + 5 v čase t = 0 dává číslo 2. Jaký je jeho význam? Je to rychlost, s jakou se pro nás mění hodnoty funkce při průchodu bodem . To je ovšem hodnota subjektivní, záleží na rychlosti, kterou se po přímce pohybujeme. Protože náš směrový vektor nemá velikost 1, náš subjektivní řez není shodný se skutečným řezem grafem, ani onen výsledek 2 proto nemá nic společného se změnou grafu funkce f.

Jak jsme již diskutovali, abychom dostali kompatibilní výsledek, musíme vyžadovat, aby se směry zadávaly pomocí vektorů velikosti 1. V našem případě bychom použili vektor

Podle výpočtu výše dostáváme, že v tomto směru se graf funkce f mění rychlostí

Toto už je také geometricky významná informace, například to opravdu souhlasí se směrnicí "tečny ve směru", tedy tečny, kterou bychom v bodě sestrojili na skutečném řezu grafem.

Pomocí tečny teď můžeme aproximovat hodnoty funkce ve směru . Pro funkci φ platí φ(t) ∼ φ(0) + φ′(0)t. Pokud toto použijeme s normalizovaným vektorem a přejdeme zpět k funkci f, dostáváme vzorec

Substitucí

dostáváme rovnocenný, ale mnohem příjemnější vzorec

Pokud nás zajímá jen aproximace, tak vlastně ani nemusíme normalizovat. Vzorec φ(t) ∼ φ(0) + φ′(0)t totiž platí pro všechny (rozumné) funkce , mimo jiné pro tu, která odpovídá původnímu směrovému vektoru , čímž hned dostaneme ten pěknější vzorec výše.

Každopádně závěr je, že pokud se chceme z bodu pohybovat jen v dotyčném směru, pak lze hodnoty funkce aproximovat (pro malá s) vzorcem

f (1 − s,2 + s) ∼ 5 + 2s.

Užitečné úvahy, které jsme právě provedli, si zaslouží oficiální zakotvení.

Definice.
Nechť f je funkce definovaná na nějakém okolí bodu ∈ℝⁿ. Nechť je vektor z ℝⁿ.

Řekneme, že funkce f je diferencovatelná v bodě ve směru , jestliže limita

konverguje.

Pak definujeme (směrovou) derivaci f v bodě ve směru jako

Je to vlastně derivace odpovídající funkce φ,

přičemž derivaci počítáme běžným způsobem. Ještě snadnější výpočet uvidíme brzy.

Jeden z výsledků onoho příkladu výše je nyní možné zachytit vzorcem D_(−1,1) f (1,2) = 2.

Definice je zavedena pro obecné směry , protože jsou aplikace, kde to má smysl (třeba fyzika), zde budeme směry normalizovat.

V úvodní části jsme uvedli, že řezy v souřadnicových směrech jsou nejpříjemnější, protože nemusíme zavádět nový parametr, pracujeme s funkcemi x ↦ (x, y₀,z₀,...), y ↦ (x₀, y,z₀,...) atd, kde navíc máme směrový vektor o normě 1, čili vše je v nejlepším možném stavu. Ony směrové vektory jsou vlastně standardní souřadnicové vektory ₁ = (1,0,...,0,0), ₂ = (0,1,...,0,0) až _n = (0,0,...,0,1), tedy obvyklá kanonická báze v ℝⁿ.

Jak by například vypadala derivace ve směru ₁, tedy ve směru osy x? Pracujeme s parametrickým vyjádřením x ↦ (x, y₀,z₀,...), máme tedy funkci φ(x) = f (x, y₀,z₀,...), kterou chceme zderivovat podle x. Vidíme, že vlastně ani žádnou novou funkci nepotřebujeme, stačí si ve funkci f zafixovat ostatní souřadnice a derivovat podle x běžným způsobem.

Příklad.
Vraťme se k funkci f (x, y) = x² + y², zajímá nás derivace ve směru osy y v bodě (1,2).

Nejprve to uděláme podle definice. Pohybujeme se po parametrické přímce t ↦  (1,2) + t(0,1) se směrovým vektorem  = (0,1), vzniká funkce φ(t) = 1² + (2 + t)² = t² + 4t + 5. Pak D f (1,2) = φ′(0) = 4.

Alternativní přístup: Vezmeme funkci f (x, y), dosadíme za x číslo 1 a výsledný vzorec f (1, y) = 1² + y² zderivujeme "podle y" běžnými pravidly: [1 + y²]′ = 2y. Nakonec dosadíme y = 2 a máme stejný výsledek.

Je vidět, že takto snadno získáme derivace obecně v libovolném bodě  = (x₀, y₀), například ve směru x ta drivace vychází derivováním funkce x² + y₀², kde teď y₀ je konstanta (neznámé, ale pevně zvolené číslo). Protože derivace konstanty y₀² (i když ji neznáme) je nula, vychází 2x, tedy derivace v bodě (x₀, y₀) ve směru osy x je 2x₀.

V praxi se ty nulky nepíšou, prostě se prohlásí, že derivace f (x, y) = x² + y² ve směru x je 2x a myslí se tím v libovolném bodě (x, y). Podobně derivace ve směru osy y je 2y. A to je celé tajemství.

Protože se tyto derivace počítají tak snadno a zároveň jde o klíčové směry, není divu, že tato myšlenka má speciální jméno.

Definice.
Nechť f je funkce definovaná na nějakém okolí bodu ∈ℝⁿ. Uvažujme jednotkové vektory _i ve směru souřadnicových os, ₁ = (1,0,0,...,0), ₂ = (0,1,0,...,0), ..., _n = (0,0,0....,1).

Pro i = 1,...,n definujeme parciální derivaci f vzhledem k x_i jako

pokud tato existuje.

V praxi se parciálně derivuje podle dané proměnné tak, že si představujeme, že všechny ostatní proměnné jsou konstanty (a tudíž i všechny výrazy, které vytvoří), a derivuje se podle dané proměnné běžnými pravidly.

Příklad.
Uvažujme funkci f (x, y,z) = x²y + sin(y³ + 2z). Najdeme všechny parciální derivace.

Parciální derivaci podle x získáme tak, že si představujeme, že y a z jsou nějaká konkrétní čísla. Protože to děláme poprvé, tak si opravdu zkusíme dát nějaká čísla místo y a z, třeba 13 a π. Pak je i sin(13³ + 2π) číslo neboli konstanta, derivováním tudíž vyjde

Stejná úvaha, ale s "y" a "z" coby konstantami, nám posytne hledaný výsledek

Obdobně si pro parciální derivaci podle y můžeme představit, že namísto x a z jsou konstanty, třeba 23 a π, a rozmyslíme si v duchu, že výpočet by pak vypadal takto:

Na papír pak napíšeme

Samozřejmě zkušený derivátor (dle vzoru "terminátor") si čísla ani nepředstavuje, prostě se naučí dobře předstírat, že někde je konstanta, a trochu si to rozmyslí. Ještě chybí derivace podle z, na to si bereme x a y jako konstanty, pak je ovšem celý člen x²y konstantní. Proto

Mimochodem, ono kroucené značení ∂, které kupodivu nemá nějaké jméno (kromě "značky pro parciální derivaci"), se dá používat stejně příjemně jako derivační čárka k indikaci derivování konkrétních výrazů, jen se značí zleva. Například u té poslední derivace můžeme použití pravidla pro derivování složené funkce vyznačit zápisem

Význam parciálních derivací

Již víme, že parciální derivace dává informace o tom, jak se funkce mění (roste, klesá) v klíčových směrech.

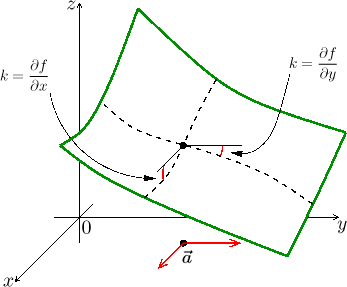
V tomto obrázku jsou obě parciální derivace záporné, takže graf klesá, pokud se z bodu posuneme ve směru souřadnicových os. Zdálo by se, že si v ostatních směrech funkce může dělat co chce, a to je obecně pravda. Pokud ovšem po funkci f požadujeme, aby se její graf "ostře nelámal", pak funkce tuto svobodu ztrácí. Poněkud překvapivě stačí docela málo, aby byl růst či klesání funkce ve všech směrech jednoznačně určen tím, jak se chová v souřadnicových směrech.

Věta.
Nechť f je funkce definovaná na nějakém okolí bodu ∈ℝⁿ. Jestliže existuje nějaké okolí bodu , že na něm pro všechna i = 1,...,n existují parciální derivace a jsou spojité v , pak má f v derivace ve všech směrech a pro každé platí

Požadavky na spojitost derivací jsou splněny často, v zásadě každá funkce zadaná algebraickým vzorcem s elementárními funkcemi (kromě absolutní hodnoty) toto splňuje, a pro takovéto funkce tedy derivaci v libovolném směru určíme čistě ze znalosti parciálních derivací. To ukazuje, že podmínka spojitých derivací má docela velké dopady.

Pro lepší manipulaci bývá zvykem schovat parciální drivace do jednoho balíčku.

Definice.
Nechť f je funkce definovaná na nějakém okolí bodu ∈ℝⁿ. Jestliže existují všechny parciální derivace () pro i = 1,...,n, pak definujeme gradient f v jako vektor

Někdy se gradient značí také jako grad( f )().

Je dobré si uvědomit, že gradient je vektor z ℝⁿ, tedy vnímáme jej jako objekt ze světa definičního oboru funkce, na symbolickém grafu jej vidíme v rámci vodorovného znázornění D( f ).

Pro funkci se spojitými derivacemi (tedy pro naprostou většinu běžně potkávaných funkcí) se závěr poslední věty výše dá elegantně napsat pomocí skalárního součinu jako

D f () = ∇ f ()•.

Příklad.
Uvažujme zase f (x, y) = x² + y². Parciální derivace jsme již počítali, tudíž hravě dostáváme gradient ∇ f (x, y) = (2x,2y).

V bodě  = (1,2) pak ∇ f (1,2) = (2,4) a vzorec dává D f (1,2) = ∇ f (1,2)•(h,k)=2h + 4k, přesně jak jsme to měli výše výpočtem podle definice.

Gradient v sobě skrývá zajímavé informace, je to jeden z klíčových pojmů.

Gradient a spád.

Představme si, že jsme v bodě , sedíme na grafu a rozhlížíme se, jak ten povrch vypadá. Podle toho, kterým směrem se díváme, graf stoupá či klesá a rychlost stoupání či klesání je dána směrovou derivací. Jinak řečeno, je dána výrazem ∇ f ()•, kde jsou jednotkové vektory. Podle známého vzorce platí

∇ f ()• = ||∇ f ()||⋅||||cos(α) = ||∇ f ()||cos(α),

kde α je úhel mezi vektory ∇ f () a .

Vidíme, že stoupáme nejrychleji, pokud se vydáme tak, aby cos(α) = 1, což je pro α = 0 neboli ve směru gradientu. Naopak největší klesání nastane v případě cos(α) = −1, tedy přesně v opačném směru.

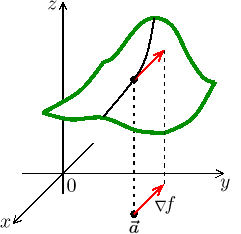
Fakt.
Nechť f je funkce, která má na okolí bodu spojité první parciální derivace. Pak gradient ∇ f () udává směr největšího růstu funkce v bodě , funkce tam roste rychlostí ||∇ f ()||.

Vektor -∇ f () udává směr největšího spádu v bodě .

Gradient a hladiny konstantnosti.

Jsme stále v bodě a sedíme na grafu. Tímto místem grafu jistě prochází nějaká úroveň, jmenovitě úroveň c =  f (), tudíž také bod leží na příslušné hladině konstantnosti (která leží v definičním oboru). Pokud se vydáme z bodu přesně tím směrem, kterým v té chvíli vede tato hladina konstantnosti (po vrstevnici), označme jej , pak oprávněně čekáme, že se hodnoty funkce alespoň chvíli nezmění (nekonečně malou, pokud máte rádi diferenciály). To znamená, že D f () = 0 neboli ||∇ f ()||cos(α) = 0 neboli α = .

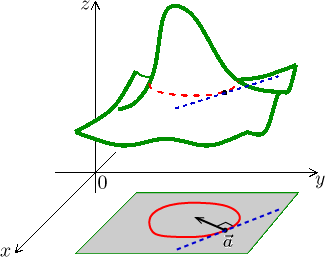
Jinými slovy, směr, kterým z bodu vychází hladina konstantnosti, je kolmý na směr nejvyššího růstu daný gradientem. Zkusme si to představit prakticky. Stojíme na úbočí hory a zvažujeme, kdy se vydat. Opravdu platí, že směr s největším stoupáním musí být kolmý na směr po vrstevnici? Umím si živě představit tvary úbočí, kdy tomu tak není. Finta je v tom, že takové úbočí coby graf funkce dvou proměných pak nesplňuje podmínku spojitosti derivací.

Fakt.
Má-li funkce f na okolí bodu spojité první parciální derivace, pak je gradient ∇ f () kolmý na hladinu konstantnosti procházející bodem .

Toto je velice užitečné. Mnohé útvary lze reprezentovat jako hladiny konstantnosti vhodné funkce, gradient pak umožňuje snadno získat kolmice k dotyčnému útvaru, což zase umožňuje pracovat s tečnými objekty.

Příklad.
Uvažujme elipsu danou rovnicí

chceme najít její tečnu v bodě (2,1).

Jedna možnost je použít přístup přes grafy. Daný bod leží na horní polovině elipsy, kde ji lze vnímat (pokud vzorec řešíme pro y) jako graf funkce

K nalezení tečny pro x = 2 potřebujeme derivaci

směrnice tečny je proto k = f ′ (2) = −1. Dostáváme přímku y − 1 = −(x − 2) neboli x + y = 3.

Alternativní přístup: Danou rovnici upravíme na příjemnější tvar x² + 2y² = 6 a rozhodneme se, že je to vlastně hladina konstantnosti funkce F(x, y) = x² + 2y² odpovídající c = 6. Najdeme gradient v bodě (2,1): ∇ F = (2x,4y), proto ∇ F(2,1) = (4,4).

Tento vektor je kolmý na dotyčnou hladinu konstantnosti neboli naši elipsu, proto je i kolmý na její tečnu. Rovnice přímky kolmé na (4,4) je 4x + 4y = d, pomocí bodu (2,1) snadno dopočítáme d = 12. Dostáváme rovnici 4x + 4y = 12 neboli x + y = 3.

Gradient a tečny, aproximace.

Již jsme si říkali, že pro funkci více proměnných nemá smysl mluvit o tečně. Když si ale představíme graf funkce dvou proměnných, napadne nás, že by mohly existovat tečné roviny. Pro funkce tří proměnných pak existují tečné třírozměrné prostory (které vypadají "ploše", když jsou zasazeny do čtyřrozměrného prostoru, ve kterém žije graf) atd. Obecně se plochému n-rozměrnému objektu v prostoru ℝⁿ⁺¹ říká (afinní) nadrovina (formálně jde o translace n-rozměrných podprostorů) a my hledáme jisté speciální.

Jak je najdeme? Tím, že se na chvíli oprostíme od geometrie a podíváme se na tečny analyticky. Víme, že u funkcí jedné proměnné je tečna v bodě a taková přímka, která nejlépe ze všech přímek aproximuje chování f okolo bodu a,

f (a + h) ∼  f (a) + f ′(a)h.

Jak bychom co nejlépe aproximovali hodnoty funkce f (x, y) okolo bodu  = (a₁,a₂)? Představme si, že se z něj o kousíček posuneme, jmenovitě o vektor  = (h,k). Jak se změní funkce?

Namísto pohybu jakoby diagonálního se do stejného místa (a₁ + h,a₂ + k) dostaneme, pokud nejprve popojdeme o h podél osy x a pak o k podél osy y. Ten první pohyb je ovšem jednorozměrná záležitost, měníme jednu proměnnou, a tam už odhadnout změnu funkce umíme, použijeme derivování v příslušném směru:

Z bodu (a₁ + h,a₂) se teď posuneme ve směru osy y o k a obdobně odhadujeme

Dáme to dohromady:

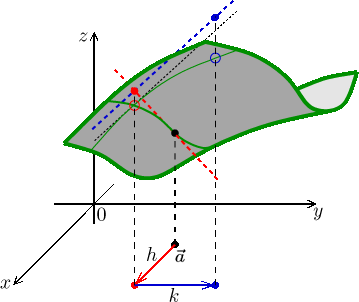
V obrázku (plochu grafu vidíme zdola) jsou hodnoty použité při aproximaci zvýrazněny plnými kolečky, zatímco správné hodnoty kroužky. Vyznačili jsme i jednotlivé tečny ve směru os použité při aproximaci.

Pokud je funkce f dostatečně pěkná, tak se při pohybu o opravdu miniaturní kousek nestačí derivace příliš změnit, proto onen posun o h v argumentu zanedbáme a dostaneme

Jinak psáno,

Výraz na pravé straně opravdu definuje rovinu a je to přesně ta, kterou jsme hledali. Její rovnice je

neboli

Je to tedy rovina daná normálovým vektorem

Obdobná úvaha platí i ve více rozměrech, máme odhad

a tečnou nadrovinu

I zde se získá standardní tvar rovnice roznásobením.

Fakt.
Nechť funkce f má spojité první derivace na okolí bodu . Jestliže vektor ∇ f () rozšíříme o jednu souřadnici navíc, jmenovitě přidáme −1 jako souřadnici (n + 1), dostaneme vektor v ℝ^n + 1 kolmý na tečnou nadrovinu ke grafu f v bodě .

Příklad.
Uvažujme f (x, y) = x² + y² a bod (1,2). Najdeme tečnou nadrovinu ke grafu f v odpovídajícím bodě.

Spočítali jsme výše, že ∇ f (1,2) = (2,4). Normálový vektor ke grafu je tedy například  = (2,4,−1).

Skrz jaký bod má tečná rovina jít? Protože f (1,2) = 5, je to bod (1,2,5). Máme bod a normálový vektor, z toho napíšeme rovnici roviny snadno:

0 = •((x, y,z) − (1,2,5)) = 2(x − 1) + 4(y − 2) − (z − 5)   =>  2x + 4y − z = 5.

Alternativa: Rovina kolmá na vektor (2,4,−1) má rovnici 2x + 4y − z + d = 0. Dosazením bodu (1,2,5) dostaneme d = −5, odtud 2x + 4y − z − 5 = 0.

Další alternativa: Graf je dán rovnicí z = x² + y². Po přepisu na tvar x² + y² − z = 0 toto lze vnímat jako hladinu konstantnosti funkce F(x, y,z) = x² + y² − z odpovídající hodnotě c = 0. Snadno najdeme ∇ F = (2x,2y,−1) a víme, že vektor ∇ F(1,2,5) = (2,4,−1) je kolmý na tuto hladinu, tedy i na náš graf a potažmo na hledanou tečnou rovinu. Její rovnice je proto

2(x − 1) + 4(y − 2) + (−1)(z − 5) = 0

a jsme hotovi.

Závěr: Tečná rovina ke grafu f v bodě daném  = (1,2) má rovnici 2x + 4y − z = 5.

Ještě si na tomto příkladě zopakujeme další poznatky o gradientu.

Funkce f poroste nejrychleji, pokud se z bodu (1,2) vydáme ve směru (2,4) neboli ve směru (1,2) (každý kladný násobek má stejný směr), rychlost růstu funkce pak bude

Bod (1,2)∈ D( f ) leží na hladině konstantnosti f (1,2) = 5 neboli na kružnici dané rovnicí y² + x² = 5. V bodě (1,2) je vektor ∇ f (1,2) = (2,4) kolmý na tuto křivku, díky čemuž hravě získáme rovnici tečny k této křivce:

0 = ∇ f (1,2)•((x, y) − (1,2)) = 2(x − 1) + 4(y − 2)   =>  2x + 4y = 10.

Z normálového směru (1,2) dostaneme známým trikem k němu kolmý vektor v ℝ², třeba (2,−1) coby směr tečný k oné hladině konstantnosti.

Parciální derivace vyššího řádu

Podobně jako u funkcí jedné proměnné, i funkce více proměnných lze derivovat vícekrát, pokud nám to funkce dovolí. Třeba u funkce f (x, y) = |x + y| v bodě (0,0) ztroskotají již první parciální derivace, zatímco na každém rozumném okolí bodu (3,2) ji lze derivovat, kolikrát se nám zachce, protože jakmile x + y > 0, pak platí f (x, y) = x + y.

Na rozdíl od případu jedné proměnné máme nicméně na výběr, dle čeho a co derivovat. U funkce dvou proměnných máme derivace prvního řádu a a obě tyto derivace můžeme následně derivovat podle x či podle y, čímž vzniknou celkem čtyři různé parciální derivace druhého řádu, například následující dvě. Ukážeme nejprve podrobný zápis postupu a pak standardní kondenzované značení:

Všimněte si pořadí derivování, symboly ve jmenovateli se berou zprava doleva, tedy začneme proměnnou nejvíce vpravo. Například parciální derivaci třetího řádu 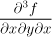bychom získali tak, že nejdříve derivujeme f podle x, výsledek pak podle y a to zase dle x, zatímco pro získání bychom nejprve derivovali podle y a pak dvakrát dle x.

Definice.
Uvažujme funkci f definovanou na okolí bodu ∈ℝⁿ. Nechť i₁,i₂,...,i_m∈{1,2...,n} jsou indexy souřadnic. Definujeme odpovídající parciální derivaci řádu m funkce f indukcí jako

za předpokladu, že všechny potřebné derivace existují.

Pokud nejsou všechny indexy souřadnic i_k stejné, pak se taková derivace nazývá smíšená.

Podobně jako u derivací prvního řádu, i vyšší derivace se dají sebrat do jednoho celku.

Definice.
Předpokládejme, že funkce f má všechny parciální derivace druhého řádu v bodě . Pak definujeme její Hessovu matici v bodě jako

Prakticky řečeno, zderivujeme funkci f dle první proměnné, tuto drivaci pak zderivujeme znovu postupně podle všech proměnných a z výsledků vytvoříme první řádek matice, obdobně pak další. Poznamenejme, že na diagonále vidíme derivace typu , zatímco mimo ni jsou derivace smíšené.

Pro shrnutí derivací třetího řádu bychom potřebovali třírozměrnou matici, jakousi krychli, čímž se dostáváme k tenzorům, které tady rozhodně nechceme probírat. V mnoha aplikacích (většině?) si vystačíme s prvními dvěma derivacemi, spokojíme se s nimi i zde.

Parciálních derivací je totiž docela dost, například pokud pracujeme s funkcí tří proměnných, tak je celkem 3⁴ = 81 parciálních derivací čtvrtého řádu. To vypadá jako spousta práce. Naštěstí máme zajímavý výsledek, který práci usnadní.

Věta.
Jestliže má funkce f všechny parciální derivace řádu m na nějakém okolí bodu a jsou všechny spojité v , pak při výpočtu konkrétní parciální drivace až po řád m nezáleží na pořadí derivování.

Mimo jiné to tedy znamená, že pokud je funkce f alespoň trochu rozumná (například zadaná vzorcem poskládaným z elementárních funkcí), tak je Hessova matice symetrická. Nabízí to určitou úsporu práce. U druhých derivací funkce dvou proměnných stačí počítat tři místo čtyř derivací, to ještě tak úžasné není a stejně bývá v praxi lepší spočítat všechny, protože shodnost smíšených funguje jako kontrola správnosti.

Výrazně lepší to ale je u vyšších řádů. Pro funkci dvou proměnných stačí počítat 4 derivace třetího řádu namísto osmi, pro funkci tří proměnných 10 derivací třetího řádu namísto 27 a 15 derivací čtvrtého řádu namísto 81. Popravdě řečeno to je spíše úspora teoretická, protože v praxi si většinou vystačíme s prvními dvěma řády, ale potěší.

Význam derivací vyššího řádu

Víme, že u funkcí jedné proměnné druhá derivace určuje znaménkem konvexitu a konkávitu funkce, velikost této derivace určuje míru zakřivení. Zde se přednášky obvykle zastaví. Jen pro zajímavost dodejme, že třetí derivace určuje vývoj konvexity/konkávity při pohledu zleva doprava. Kladná třetí derivace znamená, že se při pohledu zleva doprava zakřivení funkce "utahuje", jako když se blížíme ke středu šnekovy spirály, zatímco záporná třetí derivace signalizuje rozvolňování. O interpretaci vyšších řádů se ani nepokusíme.

Jako obvykle jsou ve více rozměrech věci ještě komplikovanější, takže se omezíme na význam druhé derivace, což už je mimochodem bonus, protože běžné kursy toto téma zcela ignorují.

Nejjednodušší je to s nesmíšenými derivacemi. Pokud graf funkce řízneme ve směru osy x, tak nám určuje konvexitu řezu, přesně jak jsme zvyklí, obdobnou informaci podávají , atd.

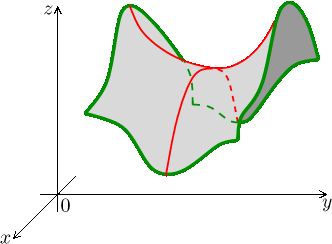
Na obrázku vidíme zajímavou situaci, kdy je funkce v jednom směru konvexní a v druhém konkávní. Dostáváme tedy smíšené sigály o chování funkce v tomto bodě a v této souvislosti se nabízí otázka, zda podobně jako u růstu grafu je již chování v dalších směrech určeno konvexitou/konkávitou v souřadnicových směrech. Je například pravda, že pokud bychom pro funkci f (x, y) v nějakém bodě dostali kladné a , tak už bude "konvexní ve všech směrech" neboli bude v dotyčném místě dolík?

Odpověď překvapivě zní, že ne, ještě se tam může dít spousta věcí, a to i když má funkce třeba spojité derivace libovolného řádu. Důvod tedy není v kvalitě funkce, ale v tom, že nesmíšené derivace druhého řádu nenesou dostatek informace. Jinými slovy, v okamžiku, kdy se začneme zajímat o zakřivení grafu, již nestačí dívat se jen na to, co se děje ve směru souřadnicových os. Potřebujeme ještě další informaci, což je přesně chvíle pro smíšené derivace.

Nejprve se podívejme na derivaci

a představme si situaci, že je kladná. Jak druhou věc v pořadí derivujeme podle y, tedy posouváme se ve směru osy y. Protože při tomto posouvání máme

znamená to, že funkce roste, tedy směrnice tečen ve směru x se zvětšují, tedy tyto tečny se vytáčejí směrem nahoru.

Umíte si představit situaci, kdy se pohybujete ve směru osy y a přitom se tečny ve směry x otáčejí směrem k většímu růstu? Takový graf je zkroucený, a to je význam smíšené druhé derivace, je to směr a míra zkroucení grafu. Ukážeme to na obrázku, na kterém se podíváme, co se děje okolo počátku.

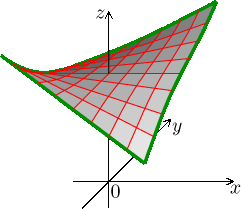
Pro zjednodušení jsme si vybrali funkci, která je na obou osách konstantní, což mimo jiné znamená, že

Vidíme proto čistě vliv smíšené druhé derivace. Abychom ten jev viděli co nejlépe, otočili jsme osy a x jde doprava, jak jsme zvyklí při znázorňování směrnice tečny. Osa y pak nutně musí jít směrem od nás.

Pokud je funkce dostatečně hladká, tak by mělo platit

měli bychom tedy dostat stejný obrázek i při interpretaci výrazu

Pokud se pohybujeme ve směru osy x, tak se směrnice tečen ve směru y stáčejí nahoru. Obrázek toto odráží, větší směrnice "ypsilonové tečny" znamená příkřejší růst ve směru osy y, tedy směrem od nás.

Právě takovéto zkroucení grafu může způsobit, že konvexita v souřadnicových směrech ještě neznamená tvar dolíku, při zkoumání zakřivení grafu je třeba (matematickým způsobem) posoudit vzájemné působení konvexity v souřadnicových směrech a zkroucení grafu indikované smíšenou derivací. Všechny složky v Hessově matici (všechny derivace druhého řádu) tedy hrají stejně důležitou roli. Na toto téma samozřejmě narazíme v části o lokálních extrémech.

Funkce více proměnných: Lokální extrémy
Zpět na Extra - Funkce více proměnných