V této části se podíváme na spojitost mezi Riemannovým a Newtonovým integrálem. Připomeňme si, že tyto integrály jsou podstatně rozdílné. Je to vidět hned na tom, že Riemannův integrál je integrál určitý, to znamená, že výsledkem je číslo, zatímco Newtonův integrál dává množinu funkcí (primitivní funkce). Riemannův integrál je geometrický pojem (plocha), zatímco Newtonův integrál je algebraický pojem. A konečně, tyto integrály jsou aplikovatelné na rozdílné množiny funkcí. Jak uvidíme, oba fungují u "pěkných" funkcí; na druhou stranu, příklad skokové funkce, který už jsme viděli předtím, je Riemannovsky integrovatelný, ale nemá primitivní funkci.
Může proto překvapit, že mezi těmito dvěma druhy integrálu je hluboká souvislost. Tomu se právě věnuje tato část. Jako jeden z důsledků obdržíme pohodlnější způsob výpočtu určitého integrálu.
Začneme definicí. Nechť f je funkce, která je Riemannovsky
integrovatelná na intervalu
![]()
Všimněte si, že jsme použili x jako horní meze, takže už jej nemůžeme
použít v integrálu a musíme si vybrat nějakou jinou proměnnou. Hodnota
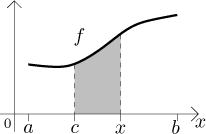
Protože číslo F(x) je definováno pro všechna x z
intervalu
Věta (Základní věta integrálního počtu 1).
Nechť f je funkce Riemannovsky integrovatelná na⟨a,b⟩, nechť c je z⟨a,b⟩. Pro x z⟨a,b⟩ definujeme
Pak F je spojitá funkce na
⟨a,b⟩. Pro x z(a,b) rovněž platí, že je-li f spojitá v x, pak F je diferencovatelná v x aF ′(x) = f (x).
Příklad: Uvažujme funkci
Nechť
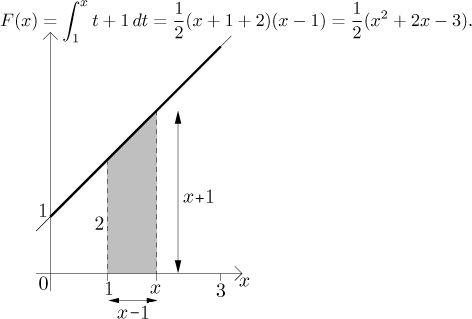
Jestliže
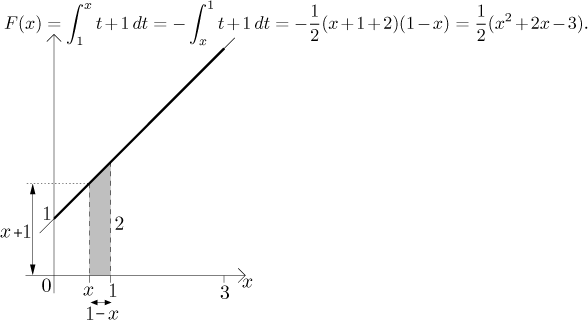
Na
![]()
Teď opravdu vidíme, že F je spojitá na
Protože většinou pracujeme právě se spojitými funkcemi a ty jsou Riemannovsky integrovatelné, máme tuto slabší ale užitečnou verzi:
Věta (Základní věta integrálního počtu 1).
Nechť f je spojitá funkce na⟨a,b⟩, nechť c je z⟨a,b⟩. Pro x z⟨a,b⟩ definujeme
Pak F je primitivní funkce k f na
⟨a,b⟩.
Teď už máme první souvislost. Vidíme, že spojité funkce jsou Riemannovsky i Newtonovsky integrovatelné a primitivní funkci (Newtonův integrál) lze dostat pomocí Riemannova integrálu. Máme ale i spojení v opačném směru:
Věta (Základní věta integrálního počtu 2).
Nechť f je spojitá funkce na⟨a,b⟩. Jestliže F je primitivní funkce k f na⟨a,b⟩, pak
Této rovnosti se říká Newton-Leibnizova formule. Protože najít primitivní funkci je skoro vždy jednodušší než pracovat s děleními intervalů, obvykle dáváme přednost počítat Riemannovy integrály právě takto. Protože se to tak často používá, při výpočtech se užívá vhodné značení:
![]()
Příklad: Víme, že
![]()
Připomeňme, že když najdeme Newtonův integrál, zapisujeme jej
![]()
Newton-Leibnizovu formuli lze použít i v případě, kdy
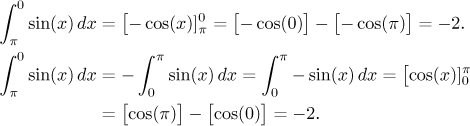
Obě Základní věty ukazují, že pro spojité funkce spolu Riemannův a Newtonův integrál souvisí. Platí i obecnější vztah.
Ten podivný integrál na začátku nespadl z čistého nebe, má totiž velice přirozenou fyzikální interpretaci. Základní věta kalkulu pak vyplyne naprosto přirozeně ze základních fyzikálních úvah, je to velice užitečný pohled na tuto problematiku a nabízíme jej v této poznámce. Zde si ukážeme užitečnou matematickou interpretaci.
Připomeňme, že když je dána funkce a my ji nejprve zintegrujeme a pak zderivujeme, tak dostaneme zase původní funkci. Když ale nejprve zderivujeme a pak zintegrujeme, tak už to nefunguje (viz Newtonův integrál v části Integrály - Teorie - Úvod). Když se ale na naše výsledky zde podíváme nikoliv z pohledu f, ale z pohledu F, pak dostaneme velice zajímavý vzorec:
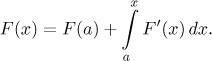
Takže pokud funkci derivujeme, tak se následnou integrací dokážeme dostat k původní funkci, pokud použijeme chytře určitý integrál.