Definition.
Consider sequences
In this section we will introduce the two main operations for sequences, namely addition (or subtraction) and multiplication by a scalar. For each of them we will explore how they affect the two properties we covered here, boundedness and monotonicity. We also briefly mention multiplication. These three operations work "term by term", which is a notion that will become clear in a second. At the end we introduce a different and less popular, yet important operation, convolution.
Having two sequences
Definition.
Consider sequences{an} and{bn}. We define their sum as
{an} + {bn} = {an + bn}. We define their difference as
{an} − {bn} = {an − bn}.
Using the long way of writing sequences (and assuming that the indexing is
Similarly it works for subtraction.
It is easy to see that addition of sequences satisfies the laws of the usual
addition. In particular, one has:
(1) the commutative law:
(2) the associative law:
(3) the zero element:
(4) the inverse element:
Here {0}n denotes the sequence
How does addition influence the properties that we studied in Theory - Introduction - Basic properties? Some general statements can be made, we list just some of the more useful:
The sum of two bounded (in any sense) sequences yields a sequence bounded in the same sense.
The difference of two bounded sequences yields a bounded sequence.
Sum of a bounded sequence and an unbounded sequence (in any sense) yields a sequence unbounded in the same sense.
The difference of a bounded sequence and an unbounded sequence yields an unbounded sequence.
The first statement is quite simple. For instance, boundedness from below
follows from the fact that if
The second statement only works with boundedness, since if we subtract two sequences, both bounded from one side only, the same for both sequences, the resulting sequence might or might not be bounded in any sense. For instance,
Here we got a sequence not bounded in any sense. However, reasons for unboundedness might cancel by substraction:
Thus the second statement is basically the only possible in this direction.
You can surely think of some examples showing that while adding a bounded and unbounded sequence preserves unboundedness in any sense, mixing bounded and unbounded sequences by subtraction can lead to many different results.
Now what about these operations and monotonicity? We have the following.
The sum of two increasing sequences is an increasing sequence.
The sum of two decreasing sequences is a decreasing sequence.
We briefly sketch the proof of the first statement.
Denote
Analogous statements work for non-increasing and non-decreasing sequences. When we add an increasing and a non-decreasing sequence, we get an increasing sequence. When we add a decreasing and a non-increasing sequence, we get a decreasing sequence. Proofs are similar to the one above.
When adding two monotone sequences of unknown type, we cannot say anything. For instance, when adding an increasing and a decreasing sequence, the tendencies of going up and going down start interacting and the stronger one wins. However, the size of steps up and down can differ throughout the sequence, so the resulting balance need not follow any monotonicity pattern. Consider the following example:
Example: Is
monotone?
Note that the first sequence is increasing and the second sequence is
decreasing. The changes follow the same pattern; going from one term to the
next, sequences always change first by one, then by three in the appropriate
direction (up for the first, down for the second sequence).
However, adding them we obtain the sequence
There are similar problems with subtraction, but general statements are still possible. For instance, if we subtract an increasing sequence from a decreasing one, we get a decreasing sequence.
Having a sequence
Definition.
Consider a sequence{an} and a real number c. We define their scalar multiple as
c{an} = {can}.
Using the long way of writing sequences (and assuming the indexing is
It is easy to see that scalar multiplication of sequences satisfies the laws
we are used to from real numbers. In particular, one has:
(1) the associative law:
(2) the distributive law:
(3) the zero element:
Since this multiplication enlarges each term of a sequence by the same ratio,
properties are basically preserved. First we dispose of a special case - the
trivial case. If
For a non-zero c everything depends on its sign. We have the
following.
If c > 0, then
c{an} has the same boundedness and monotonicity properties as the original sequence{an}.
Ifc < 0, thenc{an} has boundedness and monotonicity properties of the original sequence{an} but always of the "opposite type".
For instance, if
Example:
Consider the sequence
The sequence
This is also done term-by-term. Since we work with two sequences here, we need them to be indexed in the same way.
Definition.
Consider sequences{an} and{bn}. We define their product as
{an}⋅{bn} = {anbn}.
Using the long way of writing sequences (and assuming the indexing is
This multiplication is not very useful, however, and is rarely used. It
satisfies the laws of the usual multiplication of real numbers, including the
distributive law; as the multiplicative unit one has the sequence
Convolution is an operation that in most applications of sequences replaces multiplication. It is taken with the same priority as multiplication in algebraic calculations; in particular, it has higher priority than addition of sequences. It is usually denoted by a star. Again, it requires that the sequences be indexed in the same way. We will assume here that the indexing starts at 1.
Definition.
Consider sequences{an} and{bn}, wheren = 1,2,3,... We define their convolution as
Written in the long way it is
This may look strange but in fact it is very useful in many applications. The
idea is as follows: The first term of the convolution is one product, namely
of the first terms of the given sequences. The second term is a sum of two
products and so on. The term with index n (the n-th term) is
a sum of n products, the first product is
It is easy to see that one could also run the indexes the other way, start
with
How does the definition change if we start indexing the given sequences at a
different number, say, N? The resulting sequence will also start its
indexing with N and all the appearances of 1 in the definition of
convolution will be replaced by N. Since in many applications,
indexing
As you can see, the idea stays the same. It may be actually a bit easier if
we call the resulting sequence
The convolution satisfies the usual product rules. In particular, we
have:
(1) the commutative law:
(2) the associative law:
(3) the unit element:
(4) the distributive law:
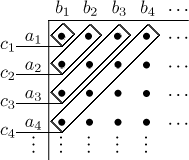
There is a handy matrix way of calculating convolution that some people like
to use. To find

To find the terms cn of the convolution, add the product along diagonals.
As an example we will calculate
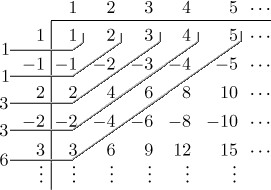
So
It is not obvious from this result how the convolution should go on, but it
seems likely that terms of the outcome come in pairs. I tried a 10 by 10
matrix and came up with
The convolution is not really used when working with sequences as such, that is, when investigating their behaviour. We will therefore refer to various applications for further study of its properties. Here in Math Tutor convolution appears in two places, namely when we introduce multiplication of series and also multiplication of power series; there is plays a crucial role.