Definition.
Consider two series,
![]() ak
ak![]() bk.
bk.
We define their sum as the series

Consider a series
![]() ak
ak
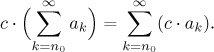
In this section we look at some properties of series, in particular we will see what is different when we pass from finite sums to infinite sums. We start with operations, then we look at "subseries" and reordering and after that we look at the basic and most important facts about convergence. At the end we look at series with non-negative terms.
When we work with objects in mathematics, we like to combine them together, for which we use various operations. We start this section by defining two most popular operations with series.
Definition.
Consider two series,and ak
bk.
We define their sum as the series
Consider a series
and a real number c. We define the product of the number and the series as ak
As you can see, we defined these operations to work "term by term", that is, we act on a series by acting on each of its terms. This is a popular way of doing things in mathematics and usually it makes good sense. This is also true now. Note that in order to be able to add two series they need to be indexed in the same way. In many cases this is just a technical problem, see reindexing in the previous section. In the definition we used the two operations to create new series, now we will show that they behave reasonably.
Theorem.
(i) If a seriesconverges, then for any real number c also the series ak
converges and (c ak)
(ii) If series
and ak
both converge, then also the series bk
converges and (ak + bk)
Since subtraction can be rewritten as summation, this theorem also works for subtraction. There are two important aspects to it.
1. We can often see the meaning of expressions with sums better if we write them in the "long notation", in this case as infinite sums. We now rewrite the two statements from the theorem, for simplicity we use indexing that starts at 1.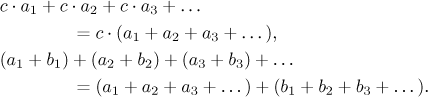
We see that the first statement is just a generalization of the distributive law from finite sums to infinite sums. The second statement is a special form of the commutative law. We will see later (see the end of the section Absolute convergence) that there is a problem with commutative law when it comes to infinite sums, what we have here is about the best we can get.
2. Unlike similar laws for finite sums, here the two equalities are "one-directional" and conditional. We can in fact go only from the right to the left in them, this especially applies to part (ii). If we know that on the right the expression makes sense (the two series converge), then and only then we can move to the left and add them up into one series. In other words, the equalities in the theorem only work sometimes, in particular when the conditions specified in this theorem are satisfied. Thus when we have a series and we want to split it into two, we are in a dangerous situation because that is exactly what the theorem does not allow us (we are trying to go "left-to-right"). When we take a series and write it as a sum of two, then the equality is not really an equality, it is a "conditional" equality in a sense that at the moment we write we do not know whether it is true. We have to check on the resulting right-hand side and if things work out there (the two series are convergent), then we know that the whole thing was correct and that equality is true; otherwise we may be doing something very wrong.
Indeed, consider the following two examples.
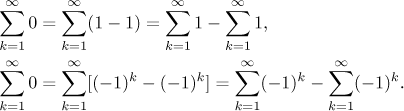
In both cases we get a nice convergent series on the left (see the previous section), but we were careless and split it into two series not very wisely. In the first case we obtained two divergent series and the expression on the right is indeterminate, infinity minus infinity. In the second case it gets even worse, since the two series on the right diverge in the worst possible way (oscillation) and we cannot even say what type the expression on the right is.
The first equality (i) is somewhat nicer, the only real trouble is when c
is zero, otherwise we can also go left to right. Indeed, if we know that the
series on the left converges and c is not zero, then by the theorem
we can multiply it by
Remark: The theorem can be stated more generally. If the expression on the right makes sense, then the equality is true.
For part (i) we therefore also get equality if the original series is infinity or minus infinity and c is not zero (recall that zero times infinity is an indeterminate expression, it also causes trouble here).
In part (ii) we know that the equality is true if the expression on the right (sum of two series) makes sense, which means that there might be two real numbers, or one real number and one (minus) infinity, or two infinities, or two negative infinities. Also adding a convergent series and a "badly" divergent series (oscillating series that do not even yield (minus) infinity) can be said to "make sense", the outcome is again a "badly" divergent series. Thus adding convergent and divergent series always works no matter what kind of divergence we have, the resulting series diverges in the same way as the divergent summand.
Fact.
If a seriesconverges and a series ak
diverges, then the series bk
diverges. (ak + bk)
Indeed, we can express
![]() bk
bk![]() (ak + bk)
(ak + bk)![]() ak,
ak,![]() bk
bk
What are the cases when the equality is not true? The example above shows the most typical ones, when the right-hand side yields infinity minus infinity or some combination of "bad divergences". Then we have no idea what happens with the series on the left, it can be convergent (for instance when two infinities cancel each other out), "nicely" divergent or "badly" divergent.
We may also run in trouble with associative law. In general, when we
introduce grouping using parentheses into a series, we can get into trouble.
For instance, recall our favorite alternating series
(1 − 1 + 1) + (−1 + 1 − 1) + ... = 1 − 1 + 1 − ...,
(1 − 1) + (1 − 1) + (1 − 1) + ... = 0 + 0 + 0 + ... = 0,
1 − (1 − 1) − (1 − 1) − (1 − 1) − ... = 1 − 0 − 0 − 0 − ... = 1.
As you can see, just by applying associative law in different ways we obtain (starting from the same series) a series that diverges and two series that converge, but each to something else. What better indication that there is something fishy with grouping? Obviously for infinite sums the "associative law" is no longer a law. Fortunately, the next statement says that if we stick to convergent series, we should be fine. Do not get scared off by the somewhat involved notation, expressing associative law properly is not simple.
Theorem (associative law).
Assume that a seriesconverges. Then for any increasing sequence ak
k1 < k2 < k3 < ... withn0 = k1 also the seriesconverges and
In the long notation:
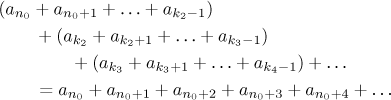
Again, this only works in the direction stated in this theorem, that is, right to left in that equality. The other direction does not work in general, it can easily happen that the grouped series on the left converges but the one on the right does not (we saw it above).
It should be noted that there is also another useful situation when we can use associative law for series. If all the terms in the series have the same sign (for instance if all the terms are non-negative), then the equality in this theorem is always true and even in both direction (see below).
Multiplication.
The natural approach is to extend multiplication as it is done for products
of finite sums. There we use the method "every term from the first part
times every term from the second part" and these products are summed up.
With series this leads to infinitely many little products of the form
Definition.
Consider two series,and ak
We define their product as the series bk.
Written in the long way,
(an0⋅bn0) + (an0⋅bn0+1 + an0+1⋅bn0) + (an0⋅bn0+2 + an0+1⋅bn0+1 + an0+2⋅bn0) + ...
This is also called the Cauchy product. Although this is the natural product, it has one unfortunate feature: It may happen that when we multiply two convergent series, then the resulting series is divergent! In order to ensure convergence of the product one has to require more, for instance that one of the two series is absolutely convergent. Then this product behaves exactly as one would expect of a "reasonable" product, namely
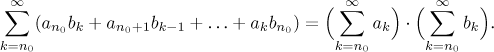
Moreover, in such a case Cauchy product satisfies the associative and commutative law and also the distributive law. All these laws are again "conditional": If the outcome of an operation makes sense, then this operation is valid.
One interesting observation: We have a series with terms
ak and a series with terms
bk. What are the terms of their product? The answer
is: It is the
convolution of the
sequences
Remark: One may also think of another natural way of multiplying two series, namely multiplication "term by term". The resulting series would be simply the sum of terms akbk. Such a multiplication is indeed possible and it also satisfies the usual rules for multiplication (commutativity, associativity). Termwise product of two convergent series is again convergent (here we have an improvement over the Cauchy product); however, its sum has nothing to do with the sums of the individual series in the product. That is, if we multiply a series which sums up to, say, 5 by a series that sums up to 2, then it is almost sure that the termwise product will not sum up to 10. This in particular shows that the notion of termwise sum is not suitable for our applications and therefore we will more or less ignore it (just like most authors).
When we have a series, sometimes we would like to sum up only some of its terms. The notation is done by picking up indices of numbers that we are interested in.
Definition.
Consider a seriesak. Let A be a subset of the set
{n0, n0 + 1, n0 + 2, n0 + 3,...}, denote its termsA = {k1 < k2 < k3 <...}. Then we define the sum over A as
Passing to a subset of terms of a series can change its behavior quite a
lot. For instance, consider the alternating series
![]() .
We know that it diverges in
the worst possible way, due to oscillation. When we take for A all
even positive integers, we get a series that sums up terms
.
We know that it diverges in
the worst possible way, due to oscillation. When we take for A all
even positive integers, we get a series that sums up terms
Of course, there is one case when we always get a convergent series in this way, namely when A is a finite set. Indeed, when we pick a finite number of terms of a series to add, we get a finite sum which always works. There is also another way to guarantee that passing to a "subseries" will work, a stronger (better and more strict) notion of convergence. For that you have to check out the section on Absolute convergence.
Pretty much the same is true for another trick we can try with a series. We already hinted above that we may have trouble with a commutative law. How do we express commutative law for series? We have some numbers and the order in which we add then up is determined by their indices, we go from smaller to larger. Thus if we want to mix the numbers up and add them in a different order (reorder them), we do it by reindexing them. Recall that if we have a set of integers considered in some order and we want to change their order, we call it a permutation. Mathematically we can represent such a permutation by a bijection P on that set.
For example, assume that we have a series and indexing of its terms goes
a1, a2, a3,
a4,..., let's say that
a3 = 13. When we sum this series up, to see the
third number in it we take
Now imagine that we want to reorder this sum in such a way that this
particular 13 is taken as the fifth term. Then we consider a permutation
P such that
Definition.
Consider a seriesBy a reordering of this series we mean any series of the form ak.
where P is some permutation of the set aP(k),
{n0, n0 + 1, n0 + 2, n0 + 3,...}.
Again we are in a funny situation that even a convergent series can be
reordered to be divergent. Note that if P is constant with exception
of finitely many terms (that is, we made only finitely many changes in the
given series), then there is some index K so that all those
changes happen before K (to put it another way,
Thus the real trouble with commutative law is in situation when we need to move infinitely many terms. Again, here we get a big help from absolute convergence.
You already saw in this section how important convergence is. Here we will present some basic results about it.
Theorem.
Consider a serieslet ak,
n1 > n0.
converges if and only if ak
converges; then also
In fact, we can say more: Two series that share terms and only differ in where they begin behave exactly the same. If one gives infinity, so does the other. If one diverges "badly" (with oscillation), so does the other. Also the equality is true "whenever it makes sense." Since the finite sum on the right is always a real number, then the right hand side makes sense for series that are convergent and also for series that give infinity or minus infinity.
This theorem has two useful consequences. First, we see that when working
with a series, we can handle its finite chunks separately whenever
convenient. More importantly, we see that the behavior of a series is
decided "at its end," its beginning does not influence it. When dealing with
series, we are often interested more in whether it converges rather than in its
actual sum (if it exists). Then we do not need to care where the indexing
starts, we can start whenever we feel like, so it becomes irrelevant.
This simplifies situation a lot and it is also reflected in notation. When
investigating convergence of a series, we do not use full notation including
index specification, we just write
Now we look closer at convergence.
Theorem (necessary condition for convergence).
If a series∑ ak converges, then necessarily the sequence{ak} converges to 0.
As the title suggests, this theorem is just an implication, so there can also be divergent sequences whose individual terms go to 0. We can also look at it in the other direction. This theorem says that if numbers ak do not go to zero, then the corresponding series is necessarily divergent. This is sometimes useful as a tool for testing convergence, but only rarely, since the really interesting series are those whose terms tend (as individuals) to zero. Then when we form a series from them, it may be convergent or divergent. In fact, such series are the really interesting ones, since then the dividing line between convergence and divergence is much more delicate.
Note that numbers ak play two different roles here,
as individuals (forming a sequence
Recall that in theoretical work we often get help from the fact that a sequence converges if and only if it is Cauchy (see Basic properties in Sequences - Theory - Limit). Applying this to partial sums of series we get the following useful criterion.
Theorem (Cauchy-Bolzano).
Consider a series∑ ak. This series converges if and only if for everyε > 0 there exists a natural number N so that for allm > n ≥ N we have
One reason why investigating convergence can get difficult is that series can behave in many different ways. However, some series are much nicer to handle.
Imagine that a given series has all its terms non-negative. This means
that as we keep adding its terms, the running totals can only increase or
at worst stay the same. In other words, the partial sums form a
non-decreasing sequence. Indeed, from
Non-decreasing sequences either converge or go to infinity (see Basic properties in Sequences - Theory - Limit), thus we get the following statement.
Theorem.
Consider a series∑ ak. Ifak ≥ 0 for all k, then either∑ ak converges or∑ ak = ∞.
We already hinted that series with non-negative terms are much better behaved when discussing associativity above, now we will state it precisely and add a statement about reorderings as a bonus.
Theorem.
Consider a seriessuch that ak
ak ≥ 0 for all k.
(i) For any increasing sequencek1 < k2 < k3 < ... withn0 = k1 the following is true:
(ii) For any reordering
the following is true: aP(k)
aP(k) =
ak.
Due to the previous Theorem, all sums in the above two equalities can be either real numbers (series converge) or infinity, and those equalities are true in all cases. Thus if in a certain equality one series sums up to infinity, then so must the one on the other side and vice versa; similarly convergence passes from one side to another. Therefore working with series with non-negative terms is very nice, the same is of course true for series with non-positive terms.
Probably the main advantage of series with non-negative terms is that their convergence is relatively easy to investigate. In fact, most tests of convergence apply only to such series. Obviously, if all numbers in a series are negative (or zero), we can always factor out the minus sign and get a series with non-negative terms, so everything that we said here also applies (with obvious modifications) to series with non-positive terms. Thus the only troublesome case is when terms in a series have different signs, which is no surprise, we already hinted that oscillating divergence is the worst.