Basic properties of real functions

Here we will introduce some basic properties of functions from a theoretical point of view. We start with boundedness, then pass to intercepts, symmetry, and periodicity. For practical information see Boundedness, Symmetry, and Periodicity in Methods Survey.

Boundedness

Definition.
We say that a real function f is bounded from below if there is a number k such that for all x from the domain D( f ) one has f (x) ≥ k.
We say that a real function f is bounded from above if there is a number K such that for all x from the domain D( f ) one has f (x) ≤ K.
We say that a real function f is bounded if it is bounded both from above and below.

Equivalently, a function f is bounded if there is a number h such that for all x from the domain D( f ) one has -h ≤ f (x) ≤ h, that is, | f (x)| ≤ h.

Being bounded from above means that there is a horizontal line such that the graph of the function lies below this line. Bounded from below means that the graph lies above some horizontal line. Being bounded means that one can enclose the whole graph between two horizontal lines. The inequalities in the definition are often shortened like this: f ≥ k, f ≤ K, and | f | ≤ h (see the note on notation at the end of the previous section).

The constants k, resp. K are called the lower, resp. upper bound for f. If there is one bound, then there is infinitely many. For instance, if f is at most 1, then also f ≤ 1.5, f ≤ 13, f ≤ 175.37, etc.

In the following picture, the function on the left seems to be bounded, while the one on the right seems to be bounded from below but not from above, therefore also not bounded. We marked some bounds that seem to work, we also tried some upper bounds in the example on the right to suggest that no bound would work (at least assuming that the function keeps going in the suggested way).

A beginner may be excused for thinking that if a function has a bounded domain (for instance if it is defined only on a closed interval, say, [1,5]), then it should be bounded, since one cannot have those growing humps like in the example on the right. However, this is not true. Even such functions need not be bounded. We refer to "Saw-like" functions in Theory - Elementary functions for examples.

The only case when the domain determines boundedness is a rather extreme one: If a function is defined only on a finite set, then it is automatically bounded, since it has only finitely many values - every finite set has a maximum and minimum. However, although such functions exist, they are freaks kept is the zoo of mathematical curiosities in order to trap unsuspecting students, one rarely meets them in applications.

For a subset M of the domain of a function f we can define boundedness on a set. The definition is similar, we want a bound (upper, lower, both) that is universal for f (x) for all x from M.

Boundednes on a set is often used and the following simple observation can come handy.

Fact.
Le f be a function bounded on some set M. Then f is also bounded on all subsets of M.

What can be said about boundedness and operations? If we add, subtract or multiply two bounded functions, then the outcome is a bounded function. If we compose two functions, and the outer one is bounded, then the whole composition is bounded.
What does not work? If we compose two functions and the inner one is bounded, the whole composition need not be bounded. For instance, the function f (x) = x² is bounded on (0,1), but when we put it into 1/x, we obtain 1/x², which is not bounded on (0,1).
Similarly, if we divide two bounded functions, the outcome need not be bounded if the one in the denominator gets arbitrarily close to 0. Example: 1/x is not bounded on (0,1), yet it is a ratio of two functions, both bounded on (0,1).

When one starts considering unbounded functions, there are lots of situations, too many to list them. There are some positive statements for boundednes above/below, most of them are common sense. For instance, adding or multiplying two functions bounded from below gives a function bounded from below. If we subtract a function bounded from below from a function bounded from above, we get a function bounded from above (write the relevant inequalities, you will see it). If we do not have even this partial boundedness, then anything is possible, for instance the sum of two such functions can be bounded, bounded above, bounded below or entirely unbounded.

One way to look closer at boundedness on a set is to ask the following question: How high and how low does f go on a given set M (a subset of the domain)?

There is an alternative way to look at these definitions. Given a function f and a set M as above, we can consider the set of all values of f on M, that is,

N = f (M) = { f (x); x∈M}.

Then sup_M( f ) = sup(N), inf_M( f ) = inf(N), max_M( f ) = max(N), and min_M( f ) = min(N).

From this it follows that the supremum and infimum always exist, but the maximum and minimum need not exist; however, if they do, they agree with supremum and infimum, respectively. We also get a direct definition of suprema and infima. For instance, sup_M( f ) is a number s satisfying the following:
    (1) f (x) ≤ s for all x from M.
    (2) For every ε > 0 there is x from M such that f (x) > s − ε.

Similar definition works for the infimum. Look at these examples:

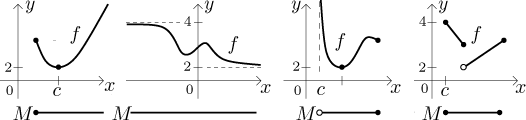
The first example: sup_M( f ) = ∞, max_M( f ) does not exist, inf_M( f ) = min_M( f ) = 2.

The second example: sup_M( f ) = 4, max_M( f ) does not exist, inf_M( f ) = 2, min_M( f ) does not exist.

The third example: sup_M( f ) = ∞, max_M( f ) does not exist, inf_M( f ) = min_M( f ) = 2.

The fourth example: sup_M( f ) = max_M( f ) = 4, inf_M( f ) = 2, min_M( f ) does not exist.

These pictures should make clear the meaning of these four notions, they should also show that minimum and maximum need not be attained even for bounded functions on bounded and closed intervals. For more information, see the next section on continuity.

Intercepts are points where the graph of f crosses the axes of the coordinate system. There are two kinds:

- x-intercepts are intersections of the graph and the x-axis. Such intercepts have coordinates (x,0), so the function must satisfy f (x) = 0. Solving this equation we find the intercepts, but it may not be easy. The solutions to this equations are also called the roots of the function or zero points of the function. See also Bisection and Newton method in Sequences - Theory - Applications. If you are curious about multiplicity of a root, look at this note.

- y-intercepts are intersections of the graph and the y-axis. Such intercepts have coordinates (0, f (0)), and since we know that a function cannot have more values for one argument, it follows that there can be at most one such intercept. We find its coordinates by substituting 0 into f (if it is possible). If 0 is not in the domain of f, then there is no y-intercept.

This property is very important, not just for drawing graphs. We focus on two kinds of symmetry, symmetry about the y-axis and symmetry about the origin. One would be also tempted to consider symmetry about the x-axis, but since a function cannot have two values for one x, this does not make sense.

Note that by a symmetric set we mean any set M satisfying the condition that if x∈M, then also (−x)∈M. Typical examples are the intervals (−K,K) or [−K,K] for some positive K, also (−∞,∞) = ℝ. Functions not defined on a symmetric interval cannot be symmetric.

Definition (symmetry).
Let f be a real function defined on a symmetric set M. We say that this function is even if for every x from M one has

f (−x) = f (x).

We say that this function is odd if for every x from M one has

f (−x) = −f (x).

Recall that the graph of f (−x) can be obtained by flipping the graph of f about the y-axis. An even function is therefore such a function that flipping its graph about the y-axis does not change its shape; in other words, the graph is symmetric about the y-axis.

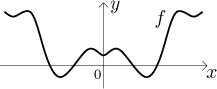
Recall also that the graph of -f (x) can be obtained by flipping the graph of f about the x-axis. An odd function is therefore such a function that flipping its graph about the y-axis gives the same outcome as flipping its graph about the x-axis. This sounds a bit confusing, so perhaps it is better to slightly change the equality: f (x) = −f (−x). This says: If we flip the graph of f about the x-axis and then about the y-axis, we get the original graph. This means that odd functions are exactly those that are symmetric with respect to the origin.

Is there a function that would be both even and odd? Yes, the function f (x) = 0 for all x.

Symmetry and operations.
Here we have some nice rules. If we add, subtract, multiply or divide two even functions, then the outcome is even. If we add or subtract two odd functions, the outcome is odd. If we multiply or divide two odd functions, then the outcome is even.

The proofs are simple, we will show a proof of the last case, since it may surprise some readers. Let f,g be two odd functions defined on a symmetric set M. Let h = f⋅g. Test of symmetry: For x∈M we have

h(−x) = f (−x)⋅g(−x) = (−f (x))⋅(−g(x)) = f (x)⋅g(x) = h(x).

Since h makes the sign disappear, it is even.

The product and ratio of two functions, one even and one odd, gives an odd function. But if we add or subtract two functions, one even and one odd, then the outcome is not a symmetric function with the exception when one of the two functions is identically zero.

What about composition? If we compose two symmetric functions, the outcome is symmetric. The kind depends on parity, the only way to get an odd function is by composing two odd functions, all other possibilities (odd-even, even-odd, even-even) lead to an even function.

We start with an informal "definition", the most typical case, to get the right feeling for the notion.

Consider a real function f defined on the whole real line. Let T be a positive number. We say that f is periodic with period T if for every real number x one has

f (x + T ) = f (x).

We also say in short that such f is T-periodic. The formula says that if we look at some point of the graph of f and jump to the right by T, the value must stay the same.

Note that once such a condition is true, then also for all integers n one has f (x + nT ) = f (x). Why is it so? Using the original equality with (x + T ) instead of x (it is also a real number) we get f (x + 2T ) = f (x + T ). Putting this together with the original equation we get f (x + 2T ) = f (x). Then we can use the original equation with (x + 2T ) instead of x and get f (x + 3T ) = f (x + 2T ) and thus f (x + 3T ) = f (x). In words, the equation allows us to jump to the right by T without changing the function value, and we can use it as many times as we want. How do we get to the left? Using the original equality with (x − T ) instead of x we get f (x) = f (x − T ), using it repeatedly we get f (x) = f (x − 2T ) etc.

The equation   f (x + nT ) = f (x)   is sometimes used as a definition of period T.

Here is an example of a 2-periodic function.

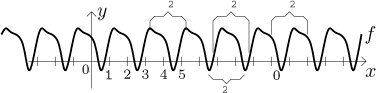
Note that once we find one period, we have infinitely many of them, since for any natural number k, every T-periodic function is also kT-periodic. Indeed, we can write

f (x + n(kT )) = f (x + (nk)T ) = f (x).

For instance, in the picture above we can also jump left and right by 4 or by 6 or... without changing the value of f. Another way to see periodicity: If we shift the graph of f to the right/left by T, the graph does not change. Yet another way to see periodicity (which is sometimes quite useful): The shape of the whole graph is determined by one piece of it. This piece has width T and the whole graph is obtained by gluing copies of this piece one after another. In the picture we marked four such possible pieces.

Once we find a period, we know that all multiples by positive integers are also periods. But sometimes we also get a period by dividing, in case we overlooked some smaller period. For instance, in the above example we may first notice the period 4 and only then realize that it is in fact just a multiple of the period 2. Is there even a smaller period such that 2 would be an integer multiple of it? Well, it does not seem to be true.

It often helps to find a basic period that gives rise to all other periods, that is, a period p so that all other periods are of the form np. Oftentimes it can be done. For instance, one can show that if we find many periods and all of them are integers, then their greatest common divisor is also a period. In the above picture, 2 seems to be the basic period. Sometimes people distinguish by saying that, in the above example, 4 is a period and 2 is the period, but it is not generally accepted; moreover, it is easy to miss such a fine distinction, and it is not even possible if we use the other way, when we say that f is 4-periodic or 2-periodic. Fortunately, it is not a problem, since in applications we rarely need to know exactly the basic period. Moreover, it can happen that no such basic period exists.

For instance, it may happen that a function has two dictinct periods and we are unable to find a common one that would work for both as basic. In some strange cases things are even stranger, for instance, the constant function f (x) = 13 has any positive real number as a period. Indeed, for any T > 0 and for any x one has f (x + T ) = 13 = f (x). Obviously, there is no basic period from which the others stem in this example. Again, such examples are rather rare and usually we meet functions which have the basic period. Sill, to see that things can get really wild, check out the Dirichlet function in Theory - Elementary functions to see a function that has all positive rational numbers as periods but no irrational period.

Quite often one would like to use the idea of periodicity (the fact that the graph is a repetition of some basic pattern) also for functions whose domain is not the whole real line. The algebraic expression would be just as above, but now one has to be careful not to jump out of the domain with argument. Here comes the definition:

Definition.
Consider a real function f. Let T be a positive number. We say that f is periodic with period T if for every real number x such that x∈D( f ) and (x + T )∈D( f ) one has

f (x + T ) = f (x).

As above, from the basic definition we get that also f (x + nT ) = f (x) for integers n, as long as the arguments in the equation belong to the domain of f. How do you imagine periodic functions now that we have this general definition? In fact the idea is very similar, the whole graph is obtained by repeating one piece of it of width T. There might be infinitely many repetitions, just now the domain may contain holes, as you can see in the following picture. We marked two possible pieces.

But there may also be just a finite number of repetitions, for instance the following function seems to be (1/2)-periodic.

What can be said about periodic functions and operations? When we add/subtract, multiply or divide two periodic functions, the outcome is again periodic. The period of the outcome is the least common multiple of the two periods. This statement says that existing periods are preserved, but it can actually happen that new ones appear. For instance, when we divide sine by cosine, both 2π-periodic, we get the tangent, which is π-periodic.

When we compose two functions and the inner function is periodic, then the whole composition is periodic. Finally, if a function f is T-periodic, then the function f (Ax) is T/|A|-periodic.

Continuity of real functions
Back to Theory - Real functions