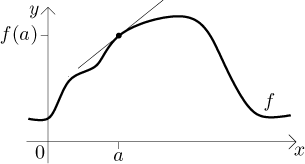
Here we first introduce derivative at a point. Then we look at derivative as a function and show some basic properties. At the end we look at one-sided derivatives.
We arrive at the notion of derivative very naturally when we ask the
following question: Consider a point
For a start, consider a nice case, a function that looks smooth and exists on some neighborhood of the given point. Intuition suggests that there should be a tangent line there.

To find the equation of this tangent line we need two pieces of data. We were given one point, for the second piece we will use the slope of the line. How do we find it? We need some approach that would allow us to use calculations (we want a precise answer, so plotting the graph and taking a guess is not acceptable). We will try the following.
We fix some number x close to (but not equal to) a and consider
the line that goes through the points
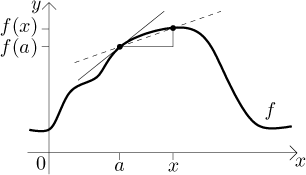
We can easily calculate the slope of this line using the outlined triangle as
![]()
Convince yourself that the same formula gives the slope also if x is to the left of a. Of course, the slope that we obtained is not exactly the same as the slope of the tangent line. However, if x is really really close to a, then we have a really good approximation. Moreover, intuitively, if we move x "all the way" to a, then the corresponding slopes should eventually give us the slope of the tangent line.
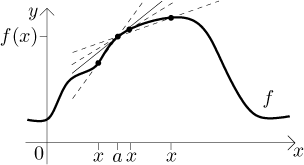
But when we speak of moving x to a we are in fact speaking of the limit. Now we are ready for the definition.
Definition.
Let f be a function defined on some neighborhood of a point a. We define the derivative of f at a by
assuming that the limit converges.
If it does converge, we say that the function is differentiable at a.
The above reasoning can be expressed as follows:
Fact.
Let f be a function defined on some neighborhood of a point a. If it is differentiable at a, then there exists the tangent line to the graph of f at a and its slope is equal tof ′(a).
Example:
We will try to find the tangent line to the graph of
![]()
To see whether there is a tangent line, we try to calculate the derivative at 1.
![]()
The limit converges, thus there is the derivative at 1 and consequently we
also have a tangent line to the graph of the root at 1. It has slope
(y − 1) = (1/2)⋅(x − 1),
which we can write for instance like this:
There is much more to derivatives than just tangent lines, in fact this whole chapter is devoted to things that can be done with derivatives, so we will leave other interesting examples for following sections. Here we will look closer at the derivative as a notion and ask some basic questions.
First, there is an alternative formula for the derivative that is more convenient in some calculations.
![]()
The equivalence of the two definitions is obvious, we just relabel the
picture above; formally one limit can be changed into the other using the
substitution
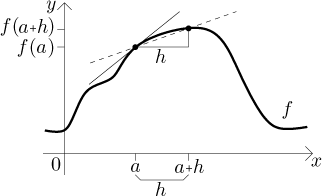
Second, the existence of a derivative is a stronger notion than that of continuity:
Theorem.
If a function is differentiable at some point, then it must be also continuous there.
However, the opposite is not true, not every continuous function is differentiable.
Example:
Consider the function

The limit does not exist, therefore the absolute value is not differentiable at 0. When we look at the picture, it seems to make sense, since there is no obvious candidate for the tangent line at the origin.
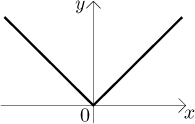
In the section on continuity in Functions - Theory - Real functions we observed that having a function continuous at one particular point does not necessarily make it "nice". The same is true about differentiability. In Dirichlet function in Functions - Theory - Elementary functions there is a weird function that is differentiable at 0 but it is not smooth anywhere, it does not even have any uninterrupted part in its graph. To really get something nice out of derivative we have to look at differentiability on intervals, which is the next part.
Definition.
Consider a function f and a subset G of its domain. We say that f is differentiable on G if it is differentiable at every point of G.
Recall that in order to have a derivative at some point, we need f to exist on some neighborhood. Thus we usually consider differentiability on open sets.
Consider a function f differentiable on some open set G.
Then for every point a of G we have a derivative
Definition.
Let a function f be differentiable at every point of some open set G. We define the function derivative of f on G as the function f ′ given bya ↦ f ′(a) for a from G.
Example:
Consider the function ![]() .
.
![]()
Thus we obtain a new function on the set
![]()
Thus we can understand the process of differentiation as a procedure that changes functions into other functions; this procedure satisfies some handy rules that will be explored in the section on Derivative and operations. They will allow us to find derivatives algebraically (that is, via an algorithm that uses a basic vocabulary and some grammar rules), which is much easier than evaluating limits. We refer to that section for further info.
We noted that differentiability at one particular point need not make a function "nice". However, now we have differentiability on a set, which is a more powerful property. Recall that a function being continuous on an interval means that the graph should be an uninterrupted curve there; however, it might still have "corners" or sharp bends on it. But if this function is also differentiable on that interval, then its graph must be "smooth", without sharp corners. By this we also suggest (again) that the existence of derivative is stronger than mere continuity. The appropriate local theorem above can be now restated globally.
Theorem.
If a function is differentiable on some open set, then it must be also continuous there.
Again, the opposite is not true, not every continuous function is differentiable.
Note the the continuity cannot be extended to endpoints. If we have a
function that is differentiable on an interval
Before we move on, we make a remark concerning the domain of the derivative
function. Since to have a derivative, we need to have the original function,
obviously the domain of f ′ must be a subset of the domain of
f. Thus the notion of domain also depends on the setting. For
instance, the function
In Functions - Theory - Real functions - Continuity we introduced the Intermediate Value Property. We have the following fact.
Theorem.
If a function is differentiable on some open interval, then its derivative has IVP there.
In that section we stated that continuous functions have IVP on intervals,
now we have another family of functions that also have it. Note that these
two types are not the same. Although it may sound weird, it can happen
that when we differentiate a function, then its derivative exists but it
is not continuous, see e.g.
Definition.
Let f be a function defined on some neighborhood of a point a. We say that f has an improper derivative at a when the limit
exists and is improper.
What is the meaning of such a derivative? Geometrically, the tangent line to the graph at that point is vertical. Derivative infinity means that the function grows, derivative negative infinity means that the function goes down.
Example:
Consider the function

So no matter what happens with the limit in derivative, now we know what it means. What else can go wrong with derivative? The very first assumption, that f exists on some neighborhood of a. There are great many different ways in which this assumption can go wrong, too many to make a system of it. However, there is one case that is so useful that it deserves its own definition. Namely, it makes sense to try a "one-sided tangent line" at endpoints of domains.
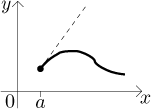
For instance, above we explored the derivative of the
square root on
Definition.
Let f be a function defined on some right neighborhood of a point a. We define the derivative from the right of f at a by
assuming that the limit converges.
Let f be a function defined on some left neighborhood of a point a. We define the derivative from the left of f at a by
assuming that the limit converges.
Example:
In the example with absolute value above we actually calculated that
One-sided derivative has the same properties as the usual derivative, all theorems that use derivative will also work for one-sided derivative, just the conclusions must be adjusted to one-sided situations. For instance:
Theorem.
If a function is differentiable from the right at some point, then it must be also continuous from the right there.
If a function is differentiable from the left at some point, then it must be also continuous from the left there.
Again, the opposite is not true.
As one would expect, one can recover the "both-sided" notion from the one-sided ones.
Theorem.
A function f is differentiable at some point a if and only if it has both derivative from the right and the derivative from the left at that point and they are equal. Then alsof ′(a) = f '+(a).
Or
We usually prefer to find one-sided derivatives using limits of derivatives rather than by definition, see Derivative and limit in Theory - MVT.
We can also define one-sided improper derivatives. Rather then giving a formal definition which is now clear anyway, we prefer to show an example.
Example:
![]()
This shows that in order to draw the graph of the square root function properly, we should start upward from the beginning at 0.

Some interpretations of derivative,
Leibniz notation
Back to Theory - Derivative