The birth process of derivatives and differential calculus in general is a fascinating story that you can find in many books. It had two fathers, Newton and Leibniz, whose followers keep arguing to this day who is the real father. Newton arrived at this notion via physics, he simply needed it so he invented it. He called it differently, but the ideas were there. The notation he introduced still survives e.g. in physics (see below). It is a bit similar to the one we use, but that one comes from Lebesgue.
Leibniz came to this notion from mathematical point of view (similar to our approach in the previous section), so he also came up with a different notation. As it happens, the two notations, f ′ and Leibniz's introduced below, are used today both in mathematics and in physics and other sciences, each has its advantages and disadvantages and we use whichever is more convenient at the moment. We will look at this in the second part of this section.
In the last part we briefly introduce some other notations used mainly in physics.
We start with the following setting. We go in a car, consider a function
Take some
![]()
In the numerator we have
Thus we see that the derivative is a limit of average velocities over smaller and smaller time intervals around our time a. It should thus seem natural that the derivative gives the instantaneous velocity at time a.
Velocity means rate of change, so this argument applies not only to f as position (or displacement), but to any quantity. When the derivative is positive, the amount we measure gets larger at a. If the derivative is negative, the measured amount gets smaller. This kind of reasoning is especially useful in physics. For instance, we just saw that the derivative of position is velocity. Likewise, the derivative of velocity is the rate of its change, that is, the acceleration. When we put it together, we see that the second derivative of position is acceleration. Thinking this way Newton arrived at the notion of derivative.
These ideas can be applied to the function f itself as a mathematical object, with no relation to physics or other applications. When we imagine the graph of f, then the derivative tells us how fast the graph goes up or down. However, this is a larger topic that has its own chapter, Graphing functions.
The notation for derivative that is most often used and that we introduced in the definition of derivative is due to Lagrange. However, there are other notations as well, the Leibniz's running close second in popularity.
The Leibniz notation for the derivative of a function
![]()
When we want to show the point at which we do the derivative, we put it as (a) after the symbol above. As usual, one can also use the notation with a vertical bar (see Introduction to functions).
![]()
Where does the Leibniz notation come from? The starting point is the question of approximation. We have a function and we know its value at a. We would like to know how much the function changes when we move that variable by a tiny bit. One natural way to approximate such a change is to use the tangent line:
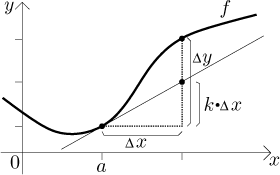
When we move the variable by
Thus we can transform the question of reasonable approximation to the question of finding the slope of the tangent line. Can we somehow get the slope using the triangles outlined in the picture?
Two things seem to be clear from the picture. First, when we make
At this point we apply a curious idea. We introduce an "infinitely small piece of the x-axis" called dx. This strange object is not a number but "something" that is smaller than all positive numbers, on the other hand it is not zero. Of course, such a strange animal does not exist, but if we imagine that it does, we get some very handy things out of it.
When we change the variable x by the "differential" dx, then
the corresponding value of f changes by differential dy in the
direction of the y-axis. Most importantly, when changing by dx
instead of by
![]()
The first notation refers to the function f by itself. We use the
second notation when we put some importance or meaning also to the second
variable
Note that there isn't just one differential for each axis. Differentials are infinitely small but they differ in size. After all, the derivative can have many possible values depending on the function, which shows that the differential dy can be smaller or larger, depending on situation. In fact, the "value" differential dy is never by itself, it is always connected to the function and point where we work; what we are mostly interested in is the mutual comparison of the sizes of dy and dx.
Assuming that the differentials make sense, we can play with them a bit to get interesting things. For instance, if we multiply out the equality above, we get
![]()
This formula is crucial in situations when we change the frame in which we
work, that is, when we change the variable. If the new variable y and
the old variable x are connected by the transformation
Similarly, the chain rule looks remarkably simple when written using the Leibniz notation. In fact, at the end of that very same section on operations you find another cute example of how the Leibniz notation makes things seem obvious. For some other situations where "differentials" seem to simplify things see this note. Note that when integrating, people usually do not bother with changing fonts and write dx instead of the proper dx, but it is the same thing.
Of course, the main problem with this approach is that infinitely small pieces do not exist. However, things seemed to work well for a long time and people were using them freely and happily, but they gradually realized that thay had getting things out of it that are not true. It was clear that calculus must be done rigorously and properly, so that it gives reliable answers. That's how we ended up with epsilons and deltas, nobody really loves them, but nothing better came along. Still, many mathematicians (and physicists etc.) still play with dx's when they think about problems, because it is very intuitive, and after they get some answers, they confirm them using the proper epsilon-delta procedure.
What are the advantages of Leibniz notation? One advantage is that it shows the variable with respect to which we differentiate. Some functions have a parameter, sometimes it is not immediately obvious which letter is a parameter and which is the variable. The Leibniz notation makes this clear. Another advantage shows up when we understand the process of differentiation as a procedure that does certain things to functions. It can be handy to have a name for this procedure, and the Leibniz notation offers one such name:
![]()
Thus we can write for instance
![]()
Remark: The "alternative analysis" is a mathematical theory that defines dx as a real mathematical object and develops rules for proper manipulation with it. Then one can use differentials and as long as the rules are observed, the conclusions are valid. However, preparing the basic groundwork for this approach (definition and investigation of dx) is not easy, so it remains one of interesting but rarely used branches of mathematics.
Since physics has been a major inspiration for calculus and physicists use derivatives very often, it is not surprising that they came up with other ways to denote it.
The dot notation. In real life situations we often mix variables that
describe space coordinates and one special variable that denotes time
(typically t). Since they play different roles, it makes sense to use
different notation for derivative to further emphasize the difference. While
the usual "apostrophe" notation is used for derivative with respect to
spatial coordinates, the derivative with respect to time is denoted by a dot
(or more dots) over the letter. The derivative of a function
![]()
By the way, this is the notation that Newton used for derivative (in general, not just with respect to time). It is nice that it still survives at least in the limited form to remain us of one of the inventors of derivative.
The subscript notation. We noted that one advantage of the Leibniz notation is that it shows the variable. However, it is also quite complicated to write, especially if you differentiate a lot. Thus we have another notation, fx denotes the derivative of f with respect to the variable x. Similarly, if f has variable y, we would write the derivative as fy.
Check out the section on higher order derivative to see how to write them using these other notations.