Problem: Find the derivative of
![]()
Solution: The function is given by a formula, so we can differentiate it using rules. The very last operation done in the given expression is the square root, that is, the given expression is of the form the square root of something. Thus we have to apply the chain rule to the composition of the outer function (square root) and the inside thing. We need to recall what the derivative of the square root is (it is handy if we remember it), or if we do not remember it, we have to deduce this rule using the elementary derivative of powers.
![]()
Now we use it with the given function (which is of the form "square root of something") and the chain rule.
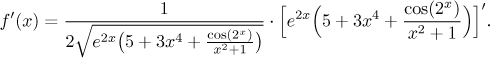
To save time and place we will replace the first fraction with a diamond shape for a while and focus on the derivative. The last operation when evaluating is multiplication (the differentiated expression is the product of two terms), so we use the product rule.
![]()
The derivative on the left is a derivative of a composed function. We apply
the chain rule, the outer function is ey whose
derivative is ey, for y we put
![]()
We take it from the left. The derivative of
[Ax + B]′ = A.
The same rule helps with [5]′. Then there is an elementary derivative of a power and finally a complicated-looking derivative. The expression inside is a fraction, so we use the quotient rule.
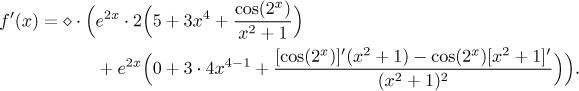
There are two derivatives to be worked out. The first one involves cosine of some function, so it is a composed function and by the chain rule we start by differentiating the outer function cosine. The second expression is differentiated easily, by linearity we differentiate each part separately, one is a standard power and the other a constant.
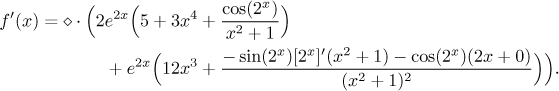
Finally we are at the end, the one derivative to be done is an elementary derivative.
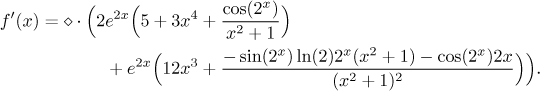
It remains to replace the diamond with the appropriate expression and find the domain of this derivative. We start by looking at the given function and take it from the inside. In the fraction the denominator is always a least 1, so no trouble there. The cosine of 2x also accepts all real numbers, so the fraction does not require any condition. The rest of the expression under the root also does not cause any trouble, so it remains to check on the square root. We need the expression under it to be at least zero. This is definitely true for the exponential at the beginning, so in order to make the whole product work we have to ensure that the big term in parentheses does not get negative. This is not one of those typical problems that can be handled by solving some equation, it is too complicated for that. We have use our experience and intuition.
What do we have there? The first two terms form a polynomial, the second one has an even power and thus it is never negative. We therefore know that the polynomial part is always at least 5. To this we add a fraction. Can it get negative? And if yes, how large does it get?
The denominator is always positive, but the numerator and thus also the fraction can sometimes be negative (what a pity). Is it possible to get a large negative number? To get this we would have to make the denominator very small or the numerator very large. However, the denominator is always at least 1, while the numerator is at most one in absolute value. Thus the fraction is at most 1 in absolute value, hence we have (for all real x)
![]()
We see that the given function exists everywhere. Now we look at the derivative. Is there any new restriction? The root should not be zero, but we already saw that it is always at least 1, so everything is fine. Thus we have
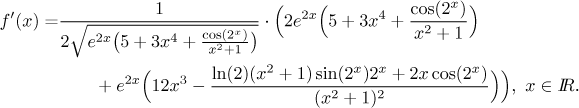
Remark: If you forget the derivative of 2x, you can always figure it out using the "e to ln" trick.
[2x]′ = [exln(2)]′ = exln(2)[xln(2)]′ = 2x⋅ln(2).