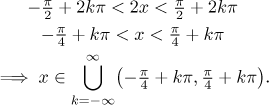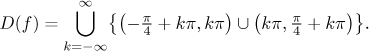Problem: Find the domain and limits at endpoints of its intervals for the function
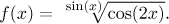
Solution: This function is a general power, so in order to investigate it we have to
change it into its canonical form first.
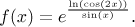
Now we look for conditions that determine the domain. The exponential can
accept anything, but in its exponent we have a logarithm and that requires
that cos(2x) be positive. There is a second condition, the
fraction expects a non-zero denominator. We look closer at the first
condition. It is an inequality featuring a trig function, so we will use some
approaches from the section Solving equations and inequalities in Extra.
First, the condition
cos(y) > 0 has the solution
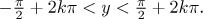
Now we substitute y = 2x
and solve for x.
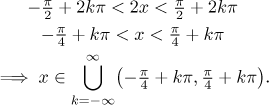
The second condition means that sin(x) is not zero, that
is, x cannot be
kπ.
Unfortunately, these points fall exactly in the middle of the intervals
above, so we have this ugly looking domain:
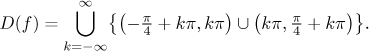
Now we need to find limits at all endpoints of intervals of this set.
There are infinitely many of them, but fortunately the given function is
2π-periodic,
which means that it is enough to find limits at endpoints of one period.
Note that one period includes two neighboring patterns from the union above,
since the period of the function is
2π, while the description of the domain above has
period π. For our
calculations we choose for instance those with
k = 0 and k = 1.
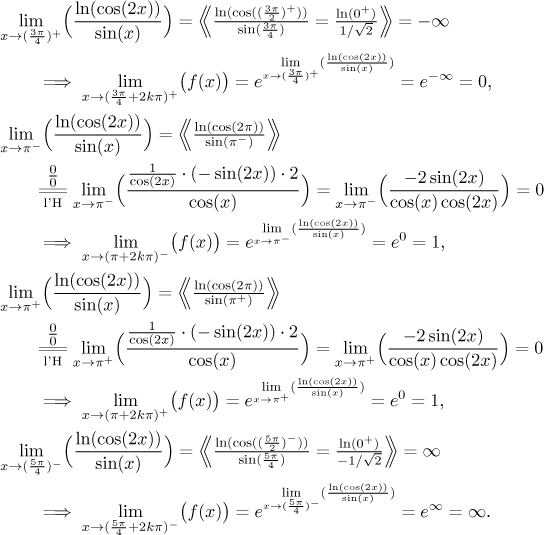
Since the function has the form of exponential, we will save time by finding
first the limit of the exponent and only then put in the exponential.

We see that we actually have a limit of f at 0, it is the common
one-sided limit 1. Analogously we do the limits for
k = 1.
We can sketch the result like this.
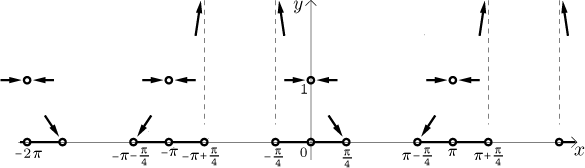
Next problem
Back to Solved Problems -
Graphing
![]()
![]()
![]()