Approximation of functions by tangent lines

Consider the following situation. We have a function f and we want to know its value at a certain point x. However, substituting x into the expression for f is not exactly pleasant, on the other hand there is a point a near x that we would not mind putting into f. Is there a way to use this to at least approximate f (x)?

In cases when substituting a into f is simple we usually also do not have a problem with substituting a into f ′. This means that we can find the tangent line T to the graph of f at a. If x is really close to a, then f (x) is very likely almost the same as T(x), so we can use the latter to approximate the former.

Solution: Although there is an algorithm for calculating square roots with a pencil and paper, almost nobody remembers it. Thus we try a different trick. We will denote the square root of x as f (x) and we will use tangent line to approximate this function. We want f (5), so we need a point a that is close to x = 5 and also is easy to put into the square root. Obviously we choose a = 4. We calculate the tangent line to f at a:

We therefore approximate the square root of 5, in other words f (5), by T(5) = 9/4 = 2.25.

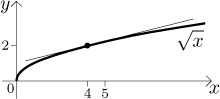
Such approximations by tangent lines are actually quite useful. People who often work with square roots of numbers close to 1 may like the approximation

which works pretty well for |x| < 0.2. In fact, you saw approximation by tangent lines in elementary or high school physics, although probably without realizing it.

Example: Consider a solid body of weight m, we will be interested in its potential energy with respect to the force of gravity of Earth. We will assume that Earth is round (with radius R) and homogeneous, which is not exactly true but close enough. Then the force F, acceleration a and potential energy U_g of such a body that has distance r from the center of the Earth is given by

However, this is not what students are taught in high-school physics. Let's simplify situation a bit. We do not really intend to bore into the Earth or move too high, so we take the radius of Earth R as the starting point. Acceleration at this radius is traditionally denoted as g, so we can put this into the acceleration equation above, express M and substitute into U_g:

Then it also makes sense to measure potential energy with respect to the surface of Earth. We will use h for the height of the solid above the surface, so r = R+h, and we introduce the relative potential energy

U(h) = U_g(R+h) - U_g(R).

We get a difference of two ratios where the variable h is in the denominator, which is not too pleasant. If we expect that the distance will not change substantially, it makes sense to try to approximate U_g by its rangent line taken at r = R, that is, for h = 0.

When we substitute this instead of U_g(R+h), we get the formula that we know from high school:

U(h) = gmh.

In fact, quite a few "laws" that we were taught in high school physics are just approximations by tangent lines of more general laws that are more complicated. The approximations usually work well within reasonable limits, for instance the potential energy formula above works reasonably well within heights that we humans most often move.

Of course, when approximating by tangent lines, we always make an error and we do not really know how large, for instance we do not know how good an estimate we got for the root of 5. For some answers (and better approximations) see the next section. For some examples see Solved Problems - Applications, an interesting application an be also found in this problem in Series - Solved Problems - Testing convergence.

Taylor polynomial
Back to Theory - Applications