In the section Basic properties in Functions - Theory - Real functions we introduced the notions of global extrema and their attaining. In general, given a function defined on a set M, the existence of maximum and minimum is not guaranteed. However, if the function is continuous on M and the set is bounded and closed, then we do have a maximum and minimum (cf. Extreme value theorem in the section Continuity in Functions - Theory - Real functions). This in particular applies to continuous functions on bounded closed intervals. On such intervals we even have a characterization of possible global extrema (we do not need continuity for that).
Theorem.
Let f be a defined on a bounded closed interval I. If f attains its global extreme at a point c, then either f has a local extreme at c or c is an endpoint of I.
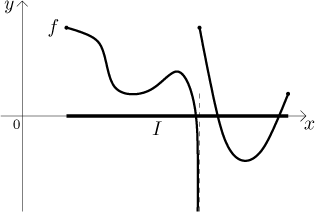
The picture shows a function which actually has two local maxima, one at an endpoint and another one that is a local maximum, we have shown here that a little discontinuity need not spoil maximum. But we also see that this particular discontinuity rules out the existence of a global minimum.

This theorem is very useful, since it narrows down the set of possible candidates. For instance, how do we find a global maximum?
1. We start with the case of a continuous function on a bounded closed interval, since then there surely is such a maximum. The first step is to collect all possible candidates, so using the theorem above we get this set by taking endpoints of the interval and adding all local extrema that lie in I, we can use derivative to find them if f is differentiable (cf. Monotonicity and local extrema in Theory - Graphing).
The second step is to choose a global maximum from among these points. How do we recognize it? Global maximum is the largest value that the function attains. Thus we simply substitute all candidates into f and compare resulting values, the largest one is the global maximum.
Obviously, when we choose the smallest value, we get the global minimum.
If the function is not continuous, then this algorithm fails. For instance, in the picture above we can compare values at endpoints and the two local minima we see there, but the smallest value is not a global minimum, since the function tends to negative infinity at the point of discontinuity (from the left). The correct answer is that the global minimum does not exist, but we do not see it from the algorithm above.
While the algorithm above is quite useful, its conditions are quite restrictive. Can we somehow relax it? One possibility is to allow for open ends in the interval. Then we cannot substitute such an endpoint, but we can find the appropriate one-sided limit at such a point and use it instead of the value. However, then we have to modify the algorithm. For instance, in the following picture we do have a global maximum on the left but there is no such thing on the right.
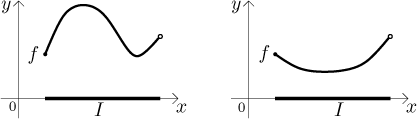
What is the difference between the two cases? In the second picture, if the interval was closed at its right endpoint, then we would have a global maximum there. But we removed that point and spoiled it all. This hints how the algorithm should be modified.
2. Now we assume that f is continuous on an interval I that need not be closed nor bounded. The first step is the same, we collect endpoints and local extrema from I. In the second step there is a change. We substitute all points from the list of candidates that are included in I, and when an endpoint is not included, we use the limit instead. Then we compare values to determine the largest/smallest. If such a value is attained at a point that belongs to I (that is, it was attained by substituting), we get an appropriate global extreme. However, if the largest/smallest value is attained only by a limit, then there is no global maximum/minimum.
We see that "missing points" complicate things only if they interfere with largest/smallest values, which we can determine by comparing limits and values obtained by substituting. This general idea can be also used to handle functions with a finite number of discontinuities. We add points of discontinuity to the list of candidates, for each of them we check on values at the points themselves and also on all possible one-sided limits. Then we compare values and if the largest value is attained only by limit(s), then there is no global maximum, similarly for minimum. Thus we get an algorithm that works for all intervals and functions that might be sometimes discontinuous. As an example we look again at the first picture, this time adding some values in the picture and making the interval unbounded on the right.
Example: Use the above algorithm to determine global extrema of
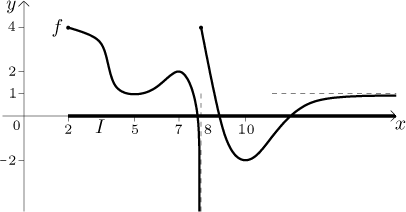
Solution: The list of candidates: endpoints 2 and infinity (there we use limit), local minima at 5 and 10, a local maximum at 7, and a point of discontinuity at 8 (there we substitute and look at one-sided limits). Values to compare:

We scan the values for the largest and find that the value 4 is actually attained as one limit and (importantly) at two points. Thus there is a global maximum, namely
The smallest "value" is
Here the problem is as follows. We are looking for global extrema of a function f, but this time f has more than one variable. However, it is actually a one-dimensional problem, since in the solution that we want the variables to satisfy some conditions, the number of conditions being one less than the number of variables.
Thus we can use these conditions to actually exclude all variables but one from the expression for f and we get a standard global extreme problem that we can solve as above.
Note that the type of problem we look at here is just a special case of a more general situation. The number of conditions need not always be one less than the number of variables, but then one has to use more advanced methods, for instance the method of Lagrange multipliers. However, this is a part of theory of functions of more variables. Here we will look only at problems that can be (using essentially common sense) transformed into problems of finding global extrema of an ordinary function.
Example: Find what dimensions of a rectangle will maximize its area, given that its perimeter must be equal to 40.
Solution: We identify data. A rectangle is given by its two adjacent
sides, so we have variables x and y. The quantity to maximize
is the area,
We use this condition to get rid of one variable in A, say
We collect all candidates. To find suspicious points for local extrema we
look at the derivative:
![]()
We obtain maximal area for
Problems of this type are called problems on optimization. In a given situation we have many possible solution, but we are looking for one that is optimal, that is, the best from a certain point of view. This point of view is described using a function, sometimes called the cost function, and we want to maximize or minimize it, depending on the situation. The constraints describe the situation under which we are optimizing.
People also call this type of question word problems, they are not exactly popular with students. Quite frankly, I am not sure why, since the principle is quite simple. I think the major obstacle is in transforming the words in the given problem to formulas. The first step (introducing appropriate variables and functions, expressing data from the "story" in mathematical terms, finding equations describing the situation) is crucial and not easy for an inexperienced student. What makes matters worse is that there is no foolproof algorithm for doing this step, every problem is different. However, once you gain some experience, it should start looking easy. For some other (more interesting?) examples see Solved Problems - Applications. For a brief overview and another example see Global extrema in Methods Survey - Applications.
Approximation of functions by tangent
lines
Back to Theory - Applications