Taylor polynomial and approximation: Survey of methods

Problem: Find the Taylor polynomial of degree n with center a for a given function f.

Case 1. The n is a concrete number.

Algorithm:
Step 1. Calculate derivatives of f up to the n-th order.
Step 2. Substitute a into all these derivatives.
Step 3. Use these numbers to create the polynomial

For more details see Taylor polynomial in Theory - Applications.

Example: Find the fourth degree Taylor polynomial with center a = 1 for f (x) = e2x.

Solution: We find the necessary derivatives and substitute a into it.

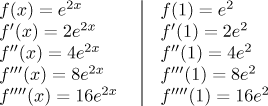
Now we create the desired polynomial.

Case 2. The n is general.

Algorithm:
Step 1. Calculate derivatives of f up to a high enough order, usually about 4 or 5 is enough.
Step 2. Substitute a into all these derivatives.
Step 3. Make a guess how the k-th derivative looks like for a general k. We only need to guess f (k)(a), so we may do the guessing after Step 2, but often it is easier to guess the general f (k)(x), since then one can see better how the derivative is shaped, only after guessing one substitutes the given center a.
Step 4. Use these numbers to create the polynomial

It might be a good idea to express it as a sum.

Example: Find the n-th degree Taylor polynomial with center a = 1 for f (x) = e2x.

Solution: We already found the first four derivatives.

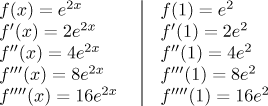
In the left column we see that at every derivative we "add" another 2 into the multiplication, we add as many of them as is the order of derivative. Thus we guess that f (k)(x) = 2ke2x, which can be proved by induction, after substituting the center we get f (k)(2) = 2ke2. We check that it fits with the first four derivatives we have above. Thus we can form the answer.

Approximation

Problem: Approximate f at a certain point b using a Taylor polynomial of the given degree.

Algorithm:
Step 1. Choose a suitable center a. Two requirements: It should be as close as possible to b and when we substitute a into f and into its derivatives, we should not have too much trouble evaluating.
Step 2. Find the Taylor polynomial of the given degree with the center a from Step 1 (see above).
Step 3. Estimate f (b) by T(b).

Example: Approximate ln(1.2) using a Taylor polynomial of degree 2.

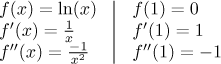
Solution: What numbers are easy to put into f (x) = ln(x)? For instance 1, e, e2, etc. The closest of them to 1.2 is a = 1. We will therefore use T2 with this center. We start by finding the necessary derivatives.

We form the polynomial:

Now we can approximate.

By the way, how precise is this estimate? We use the Lagrange form of the remainder to estimate the error.

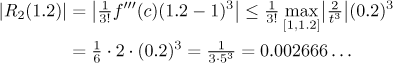
Now we know for sure that ln(1.2) = 0.180±0.003.

For other examples see Taylor polynomial in Theory - Applications and Solved Problems - Applications, an interesting application an be also found in this problem in Series - Solved Problems - Testing convergence.

An interesting special case is Taylor polynomial of degree 1, that is, a tangent line. For a useful application see Approximation of functions in Theory - Applications.

Back to Methods Survey - Applications