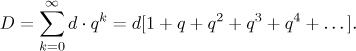
In fact, there is several of them, but the most famous of them is known as the problem of Achilles and tortoise.
Achilles was a great Greek warrior whose exploits were even quite recently known to every educated man within the world of Atlantean civilization (that is, cultures with European and Mediterranean roots). In particular he was quite fast. Now imagine that this fabled athlete sees a tortoise and for some reason decides to catch it (probably ran out of human foes to slay). We all know that he does catch it, but some 2 and half thousand years ago the philosopher Zeno of Elea advanced a rather curious theory that in fact this is not the case.
He argued like this. Achilles starts after the tortoise, but it sees him and starts "running" away. Of course Achilles is faster and soon reaches the place where tortoise was originally, but by the time he gets there, the tortoise moves somewhat further away. He keeps running and soon comes to the place where tortoise was when he reached her original place, but again, by the time he gets there, it will have moved away and is now in position three. By the time Achilles gets to position there, tortoise is already at position four. And so on ad nauseam, which proves that Achilles never catches the tortoise.
Of course, Zeno was not trying to suggest that Achilles never catches the tortoise. Greeks were arguably the first to study nature seriously and use mathematics for it (philosophers were originally people who tried to see how the world works, universal scientists if you want). However, it was not clear at the time whether math is the right tool for it, indeed the very nature of some basic things was discussed, the presented paradox was a part of a discussion on the nature of movement. Some philosophers actually argue that there are still some unresolved deep fundamental questions posed by this paradox. What is a mathematician's take on this?
Denote by d the original distance between Achilles and tortoise. Let
q be the ratio of tortoise's speed versus Achilles's speed (a number
less than 1). It is easy to see that when Achilles reaches the original
position of tortoise, then the new distance between them is
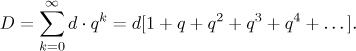
This is a
geometric series
which for
What time does it take? Denote by t the time needed for Achilles to reach the first tortoise's position (that is, t is equal to d divided by his velocity). A similar argument shows that the time needed to cover that finite distance (parceled out into infinitely many pieces) is
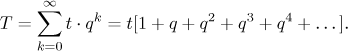
Again, this is a finite time. In this way this paradox was solved already around 200B.C.E. by Aristotle.
By the way, if Achilles is twice faster than the tortoise, then the series featured in the two formulas above is exactly the series
1 + 1/2 + 1/22 + 1/23 + 1/24 + ...
that we discussed in the introductory section. Thus this example shows that summing up such a series makes sense and corresponds to the real world.
Zeno came up with many paradoxes. Eight of them survived and are known. Five of them are said to be simple to refute, three are a bit harder and famous. One of those three we just saw, the other two are the "dichotomy argument" and the "arrow in flight" paradox. All three have a common topic. In physics (and also in other fields) we often help ourselves by decomposing more complicated situations into smaller and simpler pieces that we are then able to handle (see for instance this example). Zeno wanted to warn us that it is not quite obvious and we should do it carefully, especially the notion of movement is not as simple as it seems.
From a point of view of a mathematician (and probably of any practical natural scientist) these paradoxes are licked, calculus has the answer and methods of calculus have been shown to work for us. Some philosophers remain unconvinced, asking questions like: Granted that we calculated that the time is finite, but how can a guy manage to do infinitely many things and get to the end of them? I don't know about you, but as a student I used to feel at the end of examination session that I had just did.