Definition.
By a geometric series we mean any series of the form
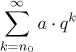
for some real constants a and q.
Here we will show two basic examples of series - the geometric series and the p-series. They are quite important, since many tests of convergence use these two types as benchmarks. At the end we look at alternating series.
We obtain geometric series by summing up a geometric sequence (see Sequences - Theory - Introduction - Important examples).
Definition.
By a geometric series we mean any series of the form
for some real constants a and q.
This is the most general definition, but many people prefer to work with
series of the form
![]() .
In fact, knowing such series is enough, since any series as in our
definition can be easily transformed into a series of this simpler form.
Indeed, we can obviously take the constant a and factor it out of the
series, so it does not influence its behavior and at the end
it can be easily factored into whatever result we get without it. The second
problem to handle is to transform the indexing so that it starts at 0. This
can be done by factoring the lowest power out of the series and then
reindexing using substitution.
.
In fact, knowing such series is enough, since any series as in our
definition can be easily transformed into a series of this simpler form.
Indeed, we can obviously take the constant a and factor it out of the
series, so it does not influence its behavior and at the end
it can be easily factored into whatever result we get without it. The second
problem to handle is to transform the indexing so that it starts at 0. This
can be done by factoring the lowest power out of the series and then
reindexing using substitution.
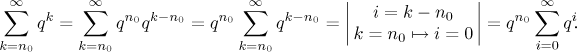
We can see better why it works if we write the series in the long way, then it is actually obvious.
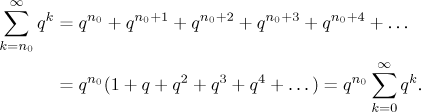
As we can see, this factoring out trick depends heavily on the fact that terms of this series are all powers with the same base, in other words, it is not going to work with other series than geometric (or those very similar to them). Anyway, since the more general form can be handily changed into the easier one and it is bother to write, in the sequel we will always use the more friendly, simpler form of a geometric series.
Geometric series is very popular, since we know all about it. Note that in
fact all examples in the first section (see
Introduction) were geometric
series. Indeed, the choice ![]() ,
the choice
,
the choice ![]() , and the
choice
, and the
choice ![]() .
Finally, the choice
.
Finally, the choice ![]() .
So what can we say about geometric series? First, using mathematical
induction we easily prove that for partial sums we have the following
formula (for q different from 1):
.
So what can we say about geometric series? First, using mathematical
induction we easily prove that for partial sums we have the following
formula (for q different from 1):
![]()
For q = 1 we have
Fact.
Consider a geometric seriesThis series converges for .
|q| < 1 and diverges for|q| ≥ 1. Moreover,
We have already shown that it is enough to know formulas for series whose index starts at 0, but some people prefer not to play with algebra and remember more general formulas instead.
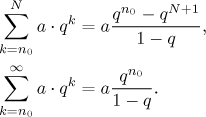
There are six basic types of geometric series, they correspond to the types described in Important examples in Sequences - Theory - Limit.
In this part we will consider series of the form
![]() , where p
is a parameter. A natural question that immediately arises is this: Why do
we write this series in this form, with terms as fractions; why don't we
write those terms in the simpler form kq? The
reason is that we want to have
, where p
is a parameter. A natural question that immediately arises is this: Why do
we write this series in this form, with terms as fractions; why don't we
write those terms in the simpler form kq? The
reason is that we want to have
Indeed, when we look at a p-series (in the above form) and ask
what happens to its terms when
What is happening when we consider positive p as advertised? Note
that when we increase p, then the numbers
Fact ( p-test).
If p > 1, then the seriesconverges.
If p ≤ 1, then.
The proof of this extremely useful
Example:
Consider the series
 .
.
The p-test says that this series is convergent
In the next section we will talk about how difficult it is to sum up a series. This series is no different, it takes quite a bit of work to show that in fact

Since all terms of this series are positive, it automatically converges absolutely and therefore we also have convergence for all modifications of signs. In particular, if we change this series into an alternating series, we get convergence and also another interesting result.
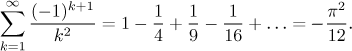
Bonus: Elementary proof that the series of
Now it seems that the series should converge and the sum should not exceed 2. This is indeed true, a rigorous proof can be obtained by a slight refinement of the above estimate (see telescopic series in the next section and comparison test in Theory - Testing convergence).
Example:
Consider the series
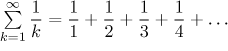 .
.
The p-test says that this series is divergent

The partial sums of the harmonic series are called harmonic numbers and denoted Hn. Their precise values are not known, despite quite a bit of research went into learning more about them. The harmonic series is rather interesting, since once we turn it into an alternating series, it becomes convergent, see the Alternating series test (in Theory - Testing convergence). We even know what the sum is (see the next section),

This alternating series converges, but when we enclose its terms in absolute values, we obtain the divergent harmonic series. Thus this is the prime example of a conditionally convergent series.
Bonus: Elementary proof that the harmonic series diverges. This proof is said to be one of the high points of medieval mathematics.
See also this note.
Remark:
This is a good opportunity to emphasize one key difference. When we have
a bunch of numbers ak, we can form two distinct
objects from them, a sequence and a series. These two need not have the
same properties. For instance, the numbers
Remark concerning subseries: Note that the series in the first
example (the one with
A bit more surprising is the fact that it can also work the other way around. For instance, we know that the alternating harmonic series is convergent. However, if we take every second term in it, we get the divergent series
![]()
The proof that it diverges is easy using limit comparison.
By an alternating series we mean any series whose terms have alternating
signs, that is, the signs in this series go
Note that sometimes we have a
natural expression of the series that has
Alternating series appear quite often and they are (relatively) simple to handle, witness the Alternating series test that we already mentioned or the last Fact in Approximating series in Theory - Introduction to Series.