Definition.
Let ![]() ak.
ak.
In this section we introduce series of real numbers and their convergence.
Definition.
Let{ak}k ≥ n0 be a sequence (of real numbers). By a series (of real numbers) we mean the abstract symbolak.
This definition is a bit weird, since we still do not know what a series is. The reason why we do it this way is that in order to learn about the meaning of this notion we have to do some work. When we say "a series", we are trying to express the idea that we have a sequence (an infinite ordered set) of real numbers a1, a2, a3, etc. (for simplicity we assume now that indexing goes 1, 2, 3,...) and we are trying to sum them up:
a1 + a2 + a3 + ...
Of course, this addition is infinite, so it never ends and it is not clear what is actually meant by it and whether it can be done at all. Can we, people living in a finite world and finite time, even contemplate infinite summations? We leave this problem to philosophers who indeed had a ball going at it and introduce one possible way of answering this question, a way that is satisfactory to most people.
The most natural approach to infinite summations is to use what we already know, that is, finite addition. Simply put, we start adding numbers in the series from the left and keep going to the right in it, adding the next and the next number, and if the running totals eventually settle down to some number, it seems natural to declare this number to be the sum of the whole series. How is this done formally? When we look at an infinite sum represented by a series, we can turn it into a finite sum by cutting off its "tail" and summing up only the first several terms.

For simplicity we again assumed that the indexing starts at 1. The index N represents the cutoff point, the corresponding finite sum is called a partial sum and denoted sN. Obviously, this number is different from the whole infinite sum, but now comes the key idea. We take the cutoff point and start moving it to the right, keep evaluating the resulting finite partial sums and look at what the resulting totals are doing. If they approach a certain value, then it makes sense to declare this value to be the sum of the infinite series. If these partial sums do not approach a certain value, then it is an indication that the series cannot be summed up in this way. The approaching business means limit.
Definition.
Consider a seriesak.
For all integers N ≥ n0 we define its partial sums by
We say that the given series converges (to A) if the sequence {sN} converges (to A). We denote it
We say that the given series diverges if the sequence {sN} diverges.
As usual, there are two special cases of divergence that are of more interest. If the sequence {sN} goes to infinity, then we say that the sum of the series is infinity and denote it

If the sequence {sN} goes to negative infinity, then we say that the sum of the series is negative infinity and denote it
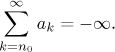
Now we have a definition, but it is not clear that it is really meaningful, since the idea that an infinite sum can make sense is weird. Are there any convergent series at all? In fact, a typical series taken at random will be divergent, but there are lots of nice convergent series. We will now look at some examples to get a feeling for this new notion.
Example:
Consider the series
![]()
This is the trivial case, even a complete series beginner would make a guess
that the sum of infinitely many zeros should be zero again. How does it work
by the definition? We try to look at the first few partial sums.
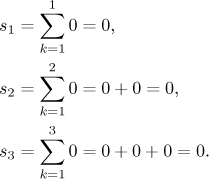
Obviously sN = 0 for all N, which is a sequence going to zero. Thus by definition we really have
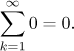
Are there more interesting examples of convergent series? Here is one known already to ancient Greeks.
Example:
Consider the series
![]() .
.
We claim that this series converges and its sum is 1. We will first use a
geometric argument to show that it can make sense. Look at the following
picture. We start with a piece of the real line representing the interval
between 0 and 1. We know that adding numbers can be represented on the real
line by putting segments of appropriate lengths one after another, and that
is exactly what we do in the picture. We start by taking a segment of length

How much is missing to 1, which is allegedly the sum of the whole series?
Obviously
Now it should be clear what is happening, at every step we fill exactly half
of what is missing to get to 1, in other words, at every step we go half the
remaining way to 1. The crucial point now is to imagine that if we keep doing
this infinitely long, until we include all numbers of the form
Although this all may look a bit unreal, infinite sums are in fact being summed up all around us and reality works exactly in the way we propose here, it is just a matter of looking at things the right way. Probably the most striking example that this summing business is in fact natural is the famous Zeno's paradox.
How does it work by the definition? We will see in the section on Important examples that the partial sum of this series is
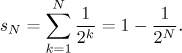
This is easy to prove using induction and agrees with our geometric approach
above. Obviously, the limit of
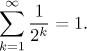
Example:
Consider the series
![]() .
.
Common sense suggests that the sum of infinitely many 1's should be
infinity. Indeed, one easily checks that partial sums are

Example:
Consider the series
![]() .
.
This series is interesting. What do we get when we start adding its terms?
We start with 1, then we add the neighboring −1 and get to 0 with our total,
then we add 1, which moves the total up, but the next term will cancel this
and we are back to 0. As we keep going to the right in our sum, the total
keeps oscillating between 1 and 0. It would seem that
the total never settles down to some number that we could reasonably call
the sum of this series. Indeed, this is true. We will now look at this by
definition.
We already saw that the outcome of a partial sum sN depends on whether N is even or odd, the formula is
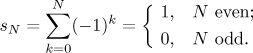
The sequence
The last two examples are very important, because they show what can cause divergence of a series. If a series is divergent, then it either attempts to sum up too much, yielding infinity (or too large numbers with negative signs giving minus infinity), or it oscillates too much; some series even manage both. This will be useful when we look closer at the problem of convergence in the next section and in Theory - Testing convergence.
Remark: There are applications when one needs a more general notion
of convergence, in particular a definition that would make also the series
from our last example convergent. There are several such more general
notions, one particularly useful assigns the compromise value
Remark: There is a nice story (Thomson's lamp) that shows how
oscillation can make it
difficult to arrive at a conclusion. Even more remarkably, this story is
made possible by the fact that a series can converge. We will use the series
from the example summing up
Since we know now that
Some people feel that this answer of "no answer" is enough, others will say that this problem has deep philosophical consequences. For instance, it shows that even if we have a complete information about an object's past, it still does not mean that we can determine its state right now. What does this imply about being able to know our world? Others say that this example is not relevant, since it uses an idealized lamp, in the real world flicking the switch takes some finite (and constant) time, so sooner or later you will not have time to flip the switch at the required speed and the whole thing goes down. Still others mean... fortunately we are mathematicians and do not have to worry about it here.
Note that indexing is in fact irrelevant. The real substance of a series is the numbers that come into it. For instance, consider the series
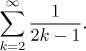
When we express it in the long notation, we get
![]()
Note that we get exactly the same when we write
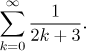
The two formal series above represent the same series shown between them, therefore they must have the same properties, they are just different expressions for the same object. The moral of the story is that we should not get too attached to some particular expression but always think of what this expression says. In fact, in many situations it helps our understanding to express a given series in the long way. Furthermore, sometimes it helps a lot if we change the expression for a given series. How does it work? We can always write the series in the long way and then try to guess some better indexing for it, but in most cases we are better served by using substitution. The basic idea is the same as substitution for other notions (limit, integral etc, see substitution). Instead of long explanations we will show how to pass from the first to the second expression above.
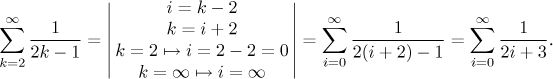
As usual, we first choose the basic substitution equality, in this case
The shift substitution does not change properties of the series.
Fact.
If we reindex a series using substitution of the formi = k + a for some integer a, then the new series has exactly the same properties as the original one.
This means that we do not make a mistake if we only consider series whose
indexing starts at
More general substitutions are possible, but they are very rarely used. One reason is that we have to be very careful about preserving the order of adding the terms and we also have to be vary of skipping some terms, see reordering in the next section.