Definition.
Consider a sequence of functions
We define its region of convergence as the set of all x for
which all fk are defined and the sequence
On this region of convergence we define the function f called the
limit of
![]()
We start with a definition of a sequence of functions and dedicate most of this section to investigating convergence, above all to the problem of preservation of properties. Eventually we will have no choice but to introduce uniform convergence. At the end we briefly look at monotonicity.
Definition.
By a sequence of functions we mean any countable ordered set
{ fk}k ≥ n0 = { fn0, fn0+1, fn0+2,...}, where fk are functions and the starting index n0 is some integer.
Depending on what kind of functions we consider, we get different theories. Here we will only consider real functions, that is, functions defined on subsets of real numbers and with real values. Another popular option is complex functions and in fact most results from here can be transferred with minor (and usually obvious) modifications to the complex case, but that is beyond the scope of Math Tutor.
Our main interest now is developing the notion of convergence for sequences
of functions, in which case we do not really care about the beginning of the
given sequence. Then - as usual - we will simplify our life by simply writing
If we want to study sequences of functions, a good start is to imagine their graphs. We have one picture with coordinate axes and we draw infinitely many graphs into this picture. If any reasonable work is to be done, we need to have at least a little place on the real line where all of these functions actually exist. That is, the whole work in this and subsequent sections is based on the usually unspoken assumption that the domains of all fk have non-empty intersection. We then work on this intersection and essentially disregard anything that happens outside this common set. So the right idea at the start is to imagine a nice set on a real line (perhaps an interval) and infinitely many functions (graphs) on it.
Before we get to the main definition, we will try to figure out what makes
actually sense. The most natural approach to sequences of any kind is to
fall back on what we know - sequences of (real) numbers. Given a sequence of
functions
When we try this for all numbers x from the intersection of domains, we
see that this intersection splits into two parts. For some x the
resulting real sequence does not converge. For some it does, these form the
region of convergence for the given sequence of functions. For each
x from this region we get the appropriate limit A of
Definition.
Consider a sequence of functions{ fk}.
We define its region of convergence as the set of all x for which all fk are defined and the sequence{ fk(x)} converges.
On this region of convergence we define the function f called the limit of{ fk} by the formula
Since the main focus now is functions, not numbers (that is, we prefer to
talk on the level of functions as abstract objects), we would like a notation
that would not refer to points. The fact that a function f is the
limit of a sequence of functions
![]()
However, we know that when dealing with functions it is crucial to know
where they live and where things work, which we do not see from the "lim"
notation. There is no widely accepted notation for the region of
convergence, in particular because we sometimes choose to work on smaller
sets anyway. Therefore we introduce the following more general convention.
If M is any subset of the region of convergence (for instance the
region itself), then we say that the sequence
We will shortly see that there are other ways to look at convergence of functions. It is generally accepted that when we talk about convergence without further specification, we mean the one we just defined, in particular because it is the basic one, other kinds of convergence usually work by adding some conditions to this notion that we already have. However, sometimes we want to emphasize that we indeed mean this convergence, that we indeed look at what is happening at individual points. Then we would say that fk converge pointwise to f on M.
Remark: When dealing with sequences of real numbers, we were also interested in a particular case of divergence, when the limit was infinite. Here this is of no interest, since the right kind of object to obtain as a limit of a sequence of functions is a function again, and we cannot assign the value infinity to a function.
Example:
Consider the sequence given by
All these functions are defined on the whole real line, so the set of real
numbers is our starting position for the investigation of the sequence of
functions
The region of convergence of the given sequence is the interval
![]()
If we call the resulting function f, then we can also write that
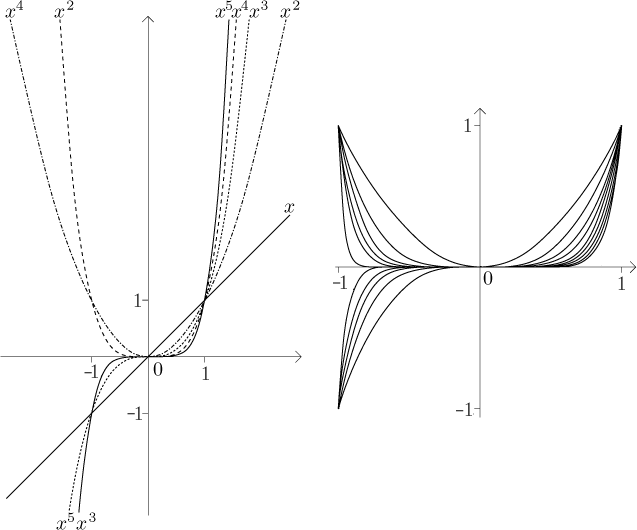
We see that the graphs of xk on
Example:
Consider the sequence given by
All these functions are defined on the whole real line, so the set of real
numbers is our starting position for the investigation of the sequence of
functions
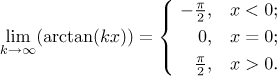
Again, a picture shows what is happening.
With growing k the curves (graphs) approach more and more constant
functions
Since the notion of convergence for functions is derived from convergence of real numbers, many nice properties are preserved. First of all, convergence of functions behaves well with respect to the usual algebraic operations.
Theorem.
Assume that a sequence of functions{ fk} converges to a function f on a set M and that a sequence of functions{gk} converges to g on the same set M. Then the following is true:
(i) For any real number a, the sequence{a⋅ fk} converges toa⋅ f on M.
(ii) The sequence{ fk + gk} converges tof + g on M.
(iii) The sequence{ fk − gk} converges tof − g on M.
(iv) The sequence{ fk⋅gk} converges tof⋅g on M.
(v) The sequence{ fk/gk} converges tof/g on the set of all x from M for which allgk(x) are not 0.
(vi) The sequence{ fkgk} converges tof g on the set of all x from M for which allfk(x) are positive.
In short, operations work whenever and wherever the outcome makes sense (for the last condition recall how we treat general powers). Note that the first two statements together combine into the statement that the notion of limit satisfies linearity.
Composition is tricky. Limit works well with composition of functions only
under some special conditions, see for instance the corresponding theorem in
the section
Basic properties
in Sequences - Theory - Limit. Therefore we will not offer any general
statement that would say something along the lines that
Theorem.
(i) Assume that a sequence of functions{ fk} converges to a function f on a set M and that a function g maps N into M. Then the sequence{ fk(g)} converges tof (g) on N.
(ii) Assume that a sequence of functions{gk} converges to a function g on a set N, a function f is continuous on M and all gk map N into M. Then the sequence{ f (gk)} converges tof (g) on N.
Some properties of functions are preserved by convergence.
Theorem.
Assume that a sequence of functions { fk} converges to a function f on a set M.
(i) If all fk are odd, then also f is odd.
(ii) If all fk are even, then also f is even.
(iii) If all fk are T-periodic, then also f is T-periodic.
(iv) If all fk are non-decreasing functions, then also f is a non-decreasing function.
(v) If all fk are non-increasing functions, then also f is a non-increasing function.
(vi) If all fk are constant functions, then also f is a constant function.
The last statement invites a clarifying remark. We talk of a sequence
of constants there. Every function as individual is a constant, but each
may be different. On the other hand, a constant sequence of functions
is a sequence where all functions are the same, but not necessarily constant
functions, For instance, if
We observed (see Functions - Theory - Limit and comparison) that passing to a limit may change inequality into equality, but never into an opposite inequality. This explains why in (iv) and (v) above monotonicity survives, but strict monotonicity does not, see below.
We saw some properties that are preserved, but unfortunately the really
interesting properties cannot be relied on to survive convergence. In
particular:
(1) even if all fk are 1-1, f need
not be 1-1;
(2) even if all fk are increasing,
f need not be increasing;
(3) even if all fk are decreasing,
f need not be decreasing;
(4) even if all fk are bounded,
f need not be bounded;
(5) even if all fk are continuous,
f need not be continuous;
(6) even if all fk are differentiable,
f need not have derivative;
(7) even if all fk are integrable,
f need not be integrable.
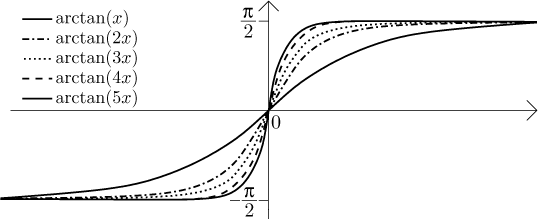
Indeed, all those arctangents in the last example are increasing,
To see that boundedness need not survive, consider this example: If we
define
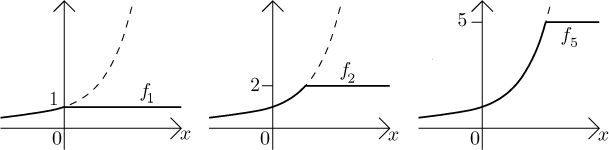
Is there any way to salvage this unpleasant situation? There are no reasonable conditions that would make (1)--(3) work. The other four can be fixed if we demand that the convergence be "better" (see the next part below). Actually, one can also fix (4) by requiring that the given sequence of functions is "uniformly bounded" and (5) by requiring that the given functions are "equicontinuous", but this is advanced stuff and we will not explore it here (it is also used much less that the "better convergence" that we do show here).
Before we get to this new convergence, we will look closer at the last three
problems (5)--(7). We will show that they in fact represent the idea of
"switching operations". With continuity it goes like this. The most
practical way of determining continuity is via limit (see
Continuity in
Functions - Theory - Real functions). Consider a sequence
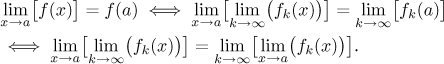
Given a sequence of functions
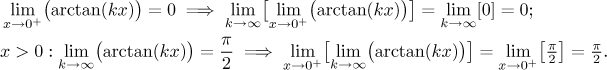
This problem appears in many situations when we can apply limit to more objects, for instance with functions of more variables, so the problem if interchangeability of limits is quite important. It is definitely worth asking under which conditions we can do it.
The derivative problem, as stated in the above list, is not exactly of this kind, but in fact we usually want more than is written there. If we have differentiable functions fk that converge to some f on a set M, we would like to know that f is differentiable and its derivative f ′ can be obtained by taking the limit of derivatives fk′. That is, we want to have a choice whether we first take the limit and then differentiate or the other way around.
![]()
This interchangeability of limit and differentiation is quite a problem as well. The above example with arctangent shows that we can lose differentiability entirely, but it can also happen that f does have a derivative, but we cannot reach it using fk, see for instance this problem in Solved Problems - Series of functions.
This brings us to the integral problem. There it is even more complicated. If integrable functions fk converge to f on some M, then we cannot hope that antiderivatives Fk would go to F for the simple and fundamental reason that every function has infinitely many antiderivatives; we may choose one for each function, but then most likely they will not form a convergent sequence as the shifts will play hell with convergence.
There are two reasonable ways out. One is to use definite integral, so one can for instance require that on any segment between a and b that lies entirely in M,

Thus we again in fact want to be able to change the order of two operations, limit and (definite) integration. The other option is to use the definite integral from some fixed a to a variable x, thus obtaining one specific choice of antiderivative, which makes good sense if the region of convergence is an interval.
Also here it may happen that f is integrable, but this integral has nothing to do with integrals of fk. Consider the following functions.
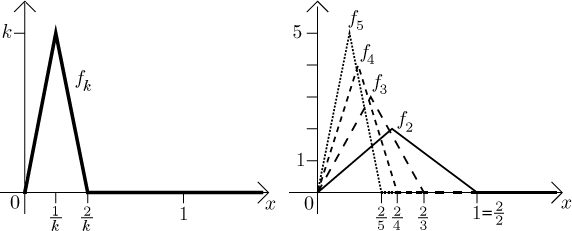
Note that as we go through this sequence, the triangles keep sliding toward 0.
Thus if we fix some positive x, sooner or later those hills pass it
and
We have shown that the last three problems (5)--(7) are related to the problem of interchanging the order of limits, differentiation and integration. Now we will get some positive results about it.
Before we show its definition, we will show why it is the right one. When we
lost continuity and more in the first two examples, the real cause was in
different speeds of convergence. For instance, we know that for
There is another way to express this. One possible interpretation of limit
is through approximation. If numbers ak converge to
A, then for every tolerance
ε there is some
aK that approximates A up to that
ε. Does it work for
functions? The first two examples show that convergence as we defined it
does not work like this. For instance, the functions
xk converge to the function 0 on
The basic idea of uniform convergence is to fix the above flaw. It allows the limit function f to be approximated arbitrarily well by a certain fk, or equivalently, it forces fk to converge to f everywhere at the same speed. The idea is simple: Instead of playing the limit game separately at every point, it is played simultaneously on the whole set of convergence.
Definition.
Consider a sequence of functions{ fk}. Let M be a set on which all fk are defined.
We say that the sequence{ fk} converges to f uniformly on M if and only if for everyε > 0 there is an integer N such that for everyk ≥ N and for every x from M:
| fk(x) − f (x)| < ε. We denote it
fk ⇉ f on M.
We start with a simple observation:
Fact.
Consider a sequence of functions{ fk} and a function f.
Iffk ⇉ f on M, thenfk→f on M.
This shows that uniform convergence is indeed stronger than pointwise
convergence and we will show below that it is strong enough to do what we
want from it. It also shows that attempting to establish uniform convergence
makes sense only on subsets of the region of convergence of
Fact.
Consider a sequence of functions{ fk} and a function f. Let M be some subset of the region of convergence of{ fk}.
Thenfk ⇉ f on M if and only if the numberssupM| fk − f | converge to 0 as k goes to infinity.
This is in fact nothing deep, just a slightly different way of writing the definition; the supremum tells us how good a particular approximation of f by some fk is globally on the set M, and we want this approximation to get as good as we need. Since the supremum can be often evaluated (or at least estimated), this is very practical. We get f from pointwise convergence and finding supremum of a function is also a standard problem.
Example:
Consider the sequence given by
We see that quality of approximations (or speed of convergence) gets really
bad near 1 and
In the last step (when evaluating the limit) we used the fact that
Similarly we easily show that in the example with sliding triangles above
the convergence is not uniform on
Uniform convergence is markedly better than pointwise convergence. For instance, recall that we had troubles with composition. With uniform convergence we do not have to worry.
Theorem.
Assume that a sequence of functions{ fk} converges uniformly to some continuous function f on a set M and that a sequence of functions{gk} converges to a function g on a set N. Assume also that all gk map N into M. Then the sequence{ fk(gk)} converges tof (g) on N.
Now we look at the properties discussed above.
Theorem.
Consider a sequence of functions{ fk} that converges to a function f.
(i) If all fk are continuous on a set M and{ fk} converges uniformly to f on M, then f is also continuous on M.
(ii) If all fk are continuous on a set M and{ fk} converges uniformly to f on M, then for every interval[a,b] that is a subset of M one has
(iii) If all fk are continuously differentiable on a set M and the sequence of derivatives
{ fk′} converges uniformly to some function g on M, then f is differentiable on M andf ′ = g.
Moreover,{ fk} actually converges to f uniformly on M.
The fact that (iii) is so complicated shows that derivatives can be quite tricky, even uniform convergence of fk is not enough to get something reasonable and one has to ask things about derivatives. Then it is just an application of a certain special version of (ii). Since this version is of some independent interest, we state it here.
Proposition.
Consider a sequence of functions{ fk} that converges uniformly to a function f on some interval M. Assume that all fk are continuous on M. Fix some a from M and for all x from M define
Then Fk converge uniformly to F on M.
We know (see e.g. the Fundamental theorem of Calculus in Integrals - Theory - Introduction) that those Fk are antiderivatives of fk and F is an antiderivative of f. Thus we see that uniform convergence of continuous (therefore integrable) functions guarantees convergence of their integrals and we had to take special antiderivatives to avoid trouble with arbitrary constants, see discussion above.
We also have a special local version of (i) that is sometimes useful.
Proposition.
Consider a sequence of functions{ fk} defined on some neighborhood of a point a. Assume that for every k,limx→a( fk(x)) = Ak for some real number Ak.
If fk converge uniformly to some function f on some neighborhood of a, then{Ak} is a convergent sequence andlimx→a( f (x)) = lim(Ak).
In short both (i) and this Proposition say that uniform convergence allows for changing the order of limits as we discussed above. Similarly, (ii) and (iii) state that under appropriate assumptions (uniform convergence at the right place) we can change the order of limit and integration, or limit and derivative.
Given a sequence of functions
Definition.
Consider a sequence of functions{ fk}, let M be some set on which all fk are defined.
(1) We say that this sequence is increasing on M if for every x from M the sequence{ fk(x)} is increasing.
(2) We say that this sequence is non-decreasing on M if for every x from M the sequence{ fk(x)} is non-decreasing.
(3) We say that this sequence is decreasing on M if for every x from M the sequence{ fk(x)} is decreasing.
(4) We say that this sequence is non-increasing on M if for every x from M the sequence{ fk(x)} is non-increasing.
We say that this sequence is monotone on M if it satisfies one of the above properties.
We say that this sequence is strictly monotone on M if it is increasing on M or decreasing on M.
In fact, here it is not necessary to do it pointwise, we can do just with
functions as objects, since in Functions - Theory - Real function -
Operations with
functions we defined comparison (inequality) for functions on sets. Thus
the sequence
As an example we take the sequence in our first example (those powers). It
is decreasing on
Uniform convergence is studied preferably on closed sets, because many things work better there (note that we also preferred statements with closed intervals above). In particular, on a closed interval one has the following interesting statement.
Theorem (Dini's theorem).
Consider a sequence of continuous functions{ fk} that converges to a continuous function f on a closed interval[a,b] for some real numbersa < b.
If the sequence{ fk} is monotone, then the convergence is uniform.