Definition.
By a series of functions we mean the symbol
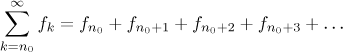
where
Given a series of functions, we define its region of convergence as
We define its region of absolute convergence as
We start with a definition of a series of functions and look at its convergence and uniform convergence. Then we address the problem of preservation of properties.
The idea of function series comes naturally when we work with Taylor polynomials. For reasonable functions, increasing the degree of Tn improves quality of approximation, so it seems that if we could somehow create an infinite Taylor polynomial, we would get precisely the original function. An infinite Taylor polynomial is an infinite sum of powers - a series. In this and subsequent sections we will show that this idea of infinite Taylor polynomial actually does work - but it takes some effort to make it work well.
When developing the notion of series for functions, we naturally take inspiration from series of numbers.
Definition.
By a series of functions we mean the symbol
where
{ fk}k ≥ n0 is some sequence of functions.Given a series of functions, we define its region of convergence as
{x real; ∑ fk(x) converges}. We define its region of absolute convergence as
{x real; ∑ fk(x) converges absolutely}.
Note that the definition makes sense. If we take some real number x
that is in domains of all fk and substitute it into
all these functions, then
Since for every x from the region of convergence we get a number - the
sum of the series
Definition.
Consider a series of functions∑ fk. Assume that f is a function defined on some set M and that all fk are also defined on this M.We say that this series converges (pointwise) to f on M if the sequence of partial sums
converges to f on M. We write
We say that this series converges to f uniformly on M if the sequence
{sN} of partial sums converges to f uniformly on M. We write
Of course, usually we want uniform convergence and convergence on the largest set possible, in the latter case on the region of convergence of course. Since convergence of series is based on convergence of sequences (of partial sums) and there uniform convergence implies pointwise convergence, we immediately obtain the following.
Proposition.
If∑ fk ⇉ f on some set M, then also∑ fk = f there.
We should actually properly write limits with the sums in this Proposition, since the concrete function f definitely depends on where the indexing starts, that is, what functions are included in the sum. For the sake of brevity we will usually skip it.
Before we show an example, we state a series version of a criterion that proved useful in case of sequences.
Proposition.
Consider a series of functions∑ fk. This series converges to some function f uniformly on a set M if and only if
Example: Investigate the series
![]() .
.
Its terms xk are defined for all real numbers, so
that's where we start. Let x be some fixed real number. If you are
not used to playing like this with x, call this fixed number
c. Then we consider the series
Next we note that if x is from
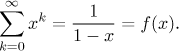
Now we would like to know whether and where this convergence is uniform. Recall that for a series with sum f, "uniform convergence on a set M" means the following: Given a tolerance, we should be able to find a partial sum of the series that approximates f on M well within that tolerance. To get some hint we first look at a picture of f and several partial sums of the given series.
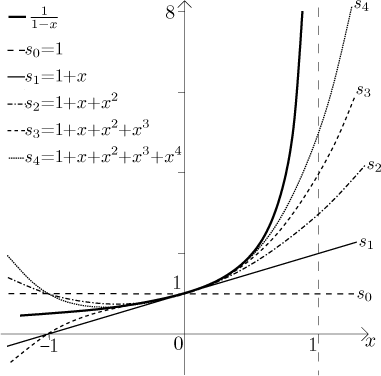
It seems that we may have trouble near 1. Indeed, we can say even without
any calculations that we definitely do not have uniform convergence on the
whole set

The fact that the supremum is infinity can be easily seen by taking limit of the expression inside at 1 from the left. Since all these suprema are infinity, there is no way they can converge to 0 when we send N to infinity.
We see that the real trouble is at 1 and also at −1 things do not look too
good (we already discussed this in the previous section, uniform convergence
is shaky at ends of the set of convergence), so what happens if we cut these
ends away? Consider some small positive number d, let
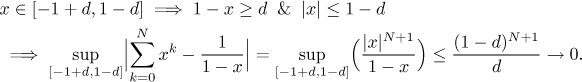
We again used the knowledge of geometric series and the fact that
This example is very instructive. In order to study uniform convergence we
need to know f, but the global approach does not help in finding it.
Thus one first needs to use the pointwise approach: Fix x and
investigate absolute convergence of the resulting real series, usually using
the Root test or the Ratio test. If we are lucky, we find that this real
series converges to some number
While in theory the situation for sequences and series is similar, in fact here we have a serious problem. We know that deciding convergence of a series is often relatively easy, so we can expect to find region of convergence fairly often. However, determining the sum of a series is in most cases a very difficult task, so finding f cannot be expected. How do we then test uniform convergence? The most popular answer is the following statement.
Theorem (the Weierstrass theorem).
Consider a series of functions∑ fk and a set M. Assume that there are real numbers ak such that∑ ak converges and
| fk(x)| ≤ ak for all k and all x from M.Then the series
∑ fk converges uniformly on M.
Using this theorem we easily show uniform convergence in the above example.
Indeed, for x from
Example: Investigate the series
![]() .
.
When we fix some real x, then it becomes a constant and we can compare the resulting series of real numbers to a known p-series to prove that it converges.
![]()
However, we have no idea what the sum of such a series with a fixed x is. Thus we know that the region of convergence of the given series of functions is the whole real line, but we do not know its sum f and the approach to uniform convergence via supremum is impossible.
However, the Weierstrass theorem works just fine, we just take M to
be the set of all real numbers and the above estimate suggests that
We still do not know to what function it converges, which may seem funny, but in fact just knowing that uniform convergence is taking place allows us to manipulate this series in many useful ways, as we will see below.
Theorem (the Dirichlet uniform convergence test).
Consider a series of functions∑ fk whose partial sums are uniformly bounded on a set M. That is, there exist a real number h such that for all x from M and for all N we have
Let
{gk} be a sequence of functions that converges uniformly to 0 on M. Then the series∑ fkgk converges uniformly on M.
Example: Investigate the series
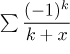 .
.
When we fix some
Now we would like to show uniform convergence on M, but the
Weierstrass theorem is no good here. We have a natural estimate
We recall that the alternating
series with terms
Theorem (the Abel uniform convergence test).
Consider a decreasing sequence of functions{ fk(x)} that are uniformly bounded on some bounded closed interval M; that is, there exists h such that| fk(x)| ≤ h for all k and all x from M.
Let∑ ak be a convergent series of real numbers. Then the series∑ ak fk converges uniformly on M.
We conclude this section with a consequence of Dini's theorem from the previous section. Note that if all functions in a given series are non-negative, then its partial sums form a non-decreasing (and therefore monotone) sequence of functions.
Theorem (Dini's theorem).
Consider a series of functions∑ fk that converges to some f on some bounded closed interval M. If all functions fk are non-negative on M, then the convergence of this series is uniform there.
We defined convergence of series using convergence of sequences, so everything that was stated about properties in the previous section carries over. As can be expected, series behave well when we apply the usual algebraic operations.
Theorem.
Assume that a series of functions∑ fk converges to a function f on a set M and that a series of functions∑ gk converges to g on the same set M. Then the following are true:
(i) For any real number a, the series∑ (a⋅ fk) converges toa⋅ f on M.
(ii) The series∑ ( fk + gk) converges tof + g on M.
(iii) The series∑ ( fk − gk) converges tof − g on M.
(iv) The series∑ ( fk⋅gk) converges on M.
Just like with real series, the pointwise multiplication in (iv) is not very useful and we prefer to multiply function series in a different way (Cauchy multiplication). We will return to this in section on power series.
The properties that were preserved for sequences are naturally also preserved here.
Theorem.
Assume that a series of functions∑ fk converges to a function f on a set M.
(i) If all fk are odd, then also f is odd.
(ii) If all fk are even, then also f is even.
(iii) If all fk are T-periodic, then also f is T-periodic.
(iv) If all fk are non-decreasing functions, then also f is a non-decreasing function.
(v) If all fk are non-increasing functions, then also f is a non-increasing function.
(vi) If all fk are constant functions, then also f is a constant function.
We know from previous section that we cannot expect preservation of continuity and other "better" properties from mere pointwise convergence (and it is easy to make up examples about it similar to those in the previous section), which is why we need uniform convergence.
Theorem.
Consider a series of functions∑ fk converging to a function f.
(i) If all fk are continuous on a set M and∑ fk converges uniformly to f on M, then f is also continuous on M.
(ii) If all fk are continuous on a set M and∑ fk converges uniformly to f on M, then for every interval[a,b] that is a subset of M one has
(iii) Assume that all fk are continuous on an interval M and that
∑ fk converges uniformly to f on M. Fix some a from M and for x from M define
Then
∑ Fk converges uniformly to F on M.(iv) If all fk are continuously differentiable on a set M and the series of their derivatives
∑ fk′ converges uniformly to some function g on M, then f is differentiable on M andf ′ = g.
Moreover,∑ fk actually converges to f uniformly on M.
Again we see that derivatives can be quite tricky, even uniform convergence of the series of fk is not enough to get something reasonable and one has to ask things about derivatives. As we discussed in the previous section, these properties are in fact rules about exchange of order of operations. We will show it in the next statement, which also shows that it can be useful to know about uniform convergence without knowing its sum and thus it justifies usefulness of the tests above. Since we are just restating the above theorem, we decided to sacrifice precision of statement to its clarity.
Proposition.
Assume that a series of functions∑ fk converges uniformly on an interval M and also that∑ fk′ converges uniformly on M if needed. Let a and b belong to M. Then
Basic systems of functions
Back to Theory - Series of functions