Operace s posloupnostmi

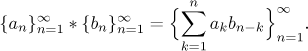
V této části uvedeme dvě hlavní operace s posloupnostmi, jmenovitě sčítání (či odčítání) a násobení konstantou. Pro každou z nich prozkoumáme, jak ovlivňují vlastnosti, které jsme zde probrali, omezenost a monotonii. Stručně se také zmíníme o násobení. Tyto operace fungují "člen po členu", což je pojem, který se záhy stane jasným. Nakonec uvedeme operaci jinou a méně populární, přesto velice důležitou: konvoluci.

Sčítání (a odčítání) posloupností

Máme-li dvě posloupnosti, {a_n} a {b_m}, sečteme je tak, že vytvoříme novou posloupnost ze součtů jednotlivých členů daných posloupností. Aby tento nápad fungoval, musí být posloupnosti indexovány stejným způsobem. Pokud jedna posloupnost začíná dříve (například pokud máme {a_n} s indexováním n = −1,0,1,2,3,... a {b_m} s indexováním m = 2,3,4,...), můžeme vždy začít tu "opožděnou" posloupnost dříve tak, že ji doplníme nulami na začátku, v našem příkladě bychom dodefinovali b₋₁ = 0, b₀ = 0, b₁ = 0, a teď už můžeme sečíst. Takový problém se ovšem nevyskytuje často. V následující definici budeme předpokládat, že posloupnosti jsou indexovány stejně, a použijeme pro ně společný index n.

Definice.
Uvažujme posloupnosti {a_n} a {b_n}. Definujeme jejich součet jako

{a_n} + {b_n} = {a_n + b_n}.

Definujeme jejich rozdíl jako

{a_n} − {b_n} = {a_n − b_n}.

Pokud použijeme dlouhý způsob zápisu (a předpokládáme, že indexování je n = 1,2,3,...), dostaneme

{a₁, a₂, a₃,...} + {b₁, b₂, b₃,...} = {a₁ + b₁, a₂ + b₂, a₃ + b₃,...}.

Podobně funguje rozdíl.

Je snadné se přesvědčit, že sčítání posloupností splňuje zákony obvyklého sčítání. Mimo jiné máme
(1)     komutativní zákon: {a_n} + {b_n} = {b_n} + {a_n},
(2)     asociativní zákon: ({a_n} + {b_n}) + {c_n} = {a_n} + ({b_n} + {c_n});
(3)     nulový prvek: {a_n} + {0}_n = {a_n},
(4)     inverzní prvek: {a_n} + {-a_n} = {0}_n.
Zde {0}_n značí posloupnost {0, 0, 0, 0,...}, neboli a_n = 0 pro všechna n.

Jak sčítání ovlivní vlastnosti, které jsme studovali v části Teorie - Úvod - Základní vlastnosti? Platí některá obecná tvrzení, vypíšeme jen ty užitečnější:

Součet dvou omezených (v libovolném smyslu) posloupností dá posloupnost omezenou ve stejném smyslu.

Rozdíl dvou omezených posloupností dá omezenou posloupnost.

Součet omezené posloupnosti s posloupností neomezenou (v libovolném smyslu) dá posloupnost neomezenou v témže smyslu.

Rozdíl omezené a neomezené posloupnosti dá neomezenou posloupnost.

První tvrzení je vlastně velmi jednoduché. Například omezenost zdola vyplývá z toho, že jestliže a_n > k a b_n > l pro všechna n, pak (a_n + b_n) > (k + l) pro všechna n.

Druhé tvrzení funguje jen s omezeností, protože když odečteme dvě posloupnosti, obě omezené jen z jedné, a to téže strany, výsledná posloupnost může a nemusí být omezená v libovolném smyslu. Například

{2, 0, 4, 0, 8, 0, 16, 0,...} − {0, 2, 0, 4, 0, 8, 0, 16,...} = {2, −2, 4, −4, 8, −8, 16, −16,...}.

Dostali jsme posloupnost neomezenou v libovolném smyslu. Je ale také možné, že se důvody neomezenosti zkrátí:

{2, 4, 8, 16,...} − {2, 4, 8, 16,...} = {0, 0, 0, 0,...}.

Druhé tvrzení je tedy v zásadě jediné možné v tomto směru.

Určitě si dokážete vymyslet příklady, které ukážou, že zatímco sečtení omezené a neomezené posloupnosti zachovává neomezenost, míchání omezených a neomezených posloupností odčítáním může vést k mnoha výsledkům.

Jak se chovají tyto operace k monotonii? Máme následující:

Součet dvou rostoucích posloupností je rostoucí posloupnost.
Součet dvou klesajících posloupností je klesající posloupnost.

Stručně dokážeme první tvrzení.

Označme {c_n} = {a_n} + {b_n}, takže pro každé n máme c_n = a_n + b_n. Protože předpokládáme, že {a_n} a {b_n} jsou rostoucí, pro každé n máme a_n+1 > a_n a b_n+1 > b_n. Pro určité n můžeme tyto nerovnosti sečíst a dostaneme a_n+1 + b_n+1 > a_n + b_n, což znamená, že c_n+1 > c_n. Tuto nerovnost jsme dokázali pro všechna n, z čehož vyplývá, že posloupnost {c_n} je rostoucí, přesně jak jsme tvrdili.

Podobná tvrzení platí o neklesajících a nerostoucích posloupnostech. Při sečtení rostoucí a neklesající posloupnosti dostaneme rostoucí, klesající a nerostoucí dává klesající. Důkazy jsou podobné.

Když sčítáme monotonní posloupnosti neznámého typu, nelze nic říct. Například při sčítání rostoucí a klesající posloupnosti se ty rostoucí a klesající tendence začnou ovlivňovat a ta silnější vyhraje. Nicméně velikosti kroků, kterými posloupnosti rostou a klesají, se mohou v průběhu posloupností měnit, takže výsledná tendence nemusí ani splňovat některý typ monotonie. Podívejme se na následující příklad:

Příklad: Je
{1, 2, 5, 6, 9, 10, 13, 14, 17, 18, 21,...} + {5, 2, 1, −2, −3, −6, −7, −10, −11, −14, −15,...}
monotonní?

Všimněte si, že první posloupnost je monotonní a druhá je klesající. Změny následují stejný vzorec; když se jde od jednoho členu k druhému, posloupnosti se střídavě pohnou nejdříve o jednu, pak o tři příslušným směrem (nahoru pro první, dolů pro druhou posloupnost).
Když je ale sečteme, dostaneme posloupnost {6, 4, 6, 4, 6, 4, 6, 4, 6, 4, 6,...}, která není monotonní.

Podobné problémy jsou s odčítáním, ale i tady jsou možné některé obecné závěry. Například když odečteme rostoucí posloupnost od klesající, dostaneme klesající posloupnost.

Násobení posloupnosti číslem

Když je dána posloupnost {a_n}, vynásobíme ji reálným číslem c tak, že vynásobíme všechny její členy číslem c.

Definice.
Uvažujme posloupnost {a_n} a reálné číslo c. Definujeme jejich skalární násobek jako

c{a_n} = {ca_n}.

Pokud použijeme dlouhý způsob psaní posloupností (a předpokládáme, že indexování je n = 1,2,3,...), můžeme psát

c{a₁, a₂, a₃,...} = {ca₁, ca₂, ca₃,...}.

Je snadné nahlédnout, že skalární násobení splňuje zákony, na které jsme zvyklí z reálných čísel. Mimo jiné máme
(1)     asociativní zákon: c(d{a_n}) = (cd){a_n};
(2)     distributivní zákon: c({a_n}+{b_n}) = c{a_n} + c{b_n};
(3)     nulový prvek: 0{a_n} = {0}_n.

Protože toto násobení zvětšuje každý člen posloupnosti stejným násobkem, vlastnosti posloupnosti jsou v zásadě zachovány. Nejprve si odbudeme speciální případ - ten triviální. Jestliže c = 0, pak c{a_n} = {0}, takže se všechny vlastnosti původní posloupnosti stanou irelevantními.
U nenulového c závisí všechno na znaménku. Platí následující:

Jestliže c > 0, pak c{a_n} má stejné vlastnosti omezenosti a monotonie jako původní posloupnost {a_n}.
Jestliže c < 0, pak c{a_n} má omezenost a monotonii původní posloupnosti {a_n}, ale vždy "opačného typu".

Například jestliže je {a_n} omezená shora, pak -{a_n} = {-a_n} je omezená zdola; jestliže je {a_n} rostoucí, pak je -{a_n} = {-a_n} klesající.

Příklad:
Uvažujme posloupnost a_n = n² − 1 pro n = 1,2,3,...; neboli posloupnost {0, 3, 8, 15, 24,...}. Tato posloupnost je omezená zdola ale ne shora, je také rostoucí.
Posloupnost (−2){n²−1} = {(−2)(n² − 1)} = {2 − 2n²}, psáno dlouhým způsobem {0, −6, −16, −30, −48,...}, je pak omezená shora, ale není omezená zdola, a je klesající.

Násobení posloupností

To se také dělá člen po členu. Protože se zde pracuje se dvěma posloupnostmi, potřebujeme, aby byly indexovány stejným způsobem.

Definice.
Uvažujme posloupnosti {a_n} a {b_n}. Definujeme jejich součin jako

{a_n}⋅{b_n} = {a_nb_n}.

Když použijeme dlouhý způsob psaní (a předpokládáme indexování n = 1,2,3,...), máme

{a₁, a₂, a₃,...}⋅{b₁, b₂, b₃,...} = {a₁b₁, a₂b₂, a₃b₃,...}.

Toto násobení ale není nějak zvlášť užitečné a je zřídkakdy používané. Splňuje obvyklé zákony násobení reálných čísel včetně distributivního; coby multiplikativní jednotku máme posloupnost {1}_n = {1, 1, 1,...}.

Konvoluce je operace, která ve většině aplikací posloupností nahrazuje násobení. V algebraických výpočtech se bere s toutéž prioritou jako násobení; mimo jiné má tedy vyšší prioritu než sčítání posloupností. Obvykle se značí hvězdičkou. Zase zde vyžadujeme, aby byly posloupnosti indexovány stejným způsobem. Budeme teď předpokládat, že indexace začíná jedničkou.

Definice.
Uvažujme posloupnosti {a_n} a {b_n}, kde n = 1,2,3,... Definujeme jejich konvoluci jako

Psáno dlouhým způsobem to je

{a₁, a₂, a₃,...} * {b₁, b₂, b₃,...} = {a₁b₁, a₁b₂ + a₂b₁, a₁b₃ + a₂b₂ + a₃b₁,...}.

Možná to vypadá podivně, ale je to velmi užitečné v mnoha aplikacích. Princip je následující: První člen konvoluce je jeden součin, jmenovitě součin prvních členů daných posloupností. Druhý člen je součet dvou součinů a tak dále. Člen s indexem n (n-tý člen) je součet n součinů, první součin je a₁b_n, pak se začne zároveň přidávat index u a ubírat index u b po jedné, dokud se zcela neprohodí, to jest dokud se nedostaneme k a_nb₁.
Je jasné, že se indexy také dají brát naopak, začít s a_nb₁ a skončit s a₁b_n.

Jak se definice změní, pokud indexování daných posloupností začíná jiným číslem, například N? Výsledná posloupnost pak také začíná index u N a všechny výskyty čísla 1 v definici konvoluce se nahradí N. Protože se v mnoha aplikacích vyžaduje indexování n = 0,1,2,3..., ukážeme, jak to pak vypadá:

{a₀, a₁, a₂,...} * {b₀, b₁, b₂,...} = {a₀b₀, a₀b₁ + a₁b₀, a₀b₂ + a₁b₁ + a₂b₀,...}.

Jak vidíte, základní myšlenka zůstává. Možná je trochu jednodušší, když se výsledná posloupnost označí {c_n} a vypíší její členy:
c₀ = a₀b₀,
c₁ = a₀b₁ + a₁b₀,
c₂ = a₀b₂ + a₁b₁ + a₂b₀,...

Konvoluce splňuje obvyklá pravidla násobení. Mimo jiné máme:
(1)     komutativní zákon: {a_n} * {b_n} = {b_n} * {a_n},
(2)     asociativní zákon: ({a_n} * {b_n}) * {c_n} = {a_n} * ({b_n} * {c_n});
(3)     jednotkový prvek: {a_n} * {1, 0, 0, 0, 0,...} = {a_n},
(4)     distributivní zákon: ({a_n} + {b_n}) * {c_n}={a_n} * {c_n} + {b_n} * {c_n}.

Existuje docela pohodlný způsob počítání konvoluce, kterému dávají někteří lidé přednost. Abychom našli {c_n} = {a_n} * {b_n}, začneme tím, že vypíšeme členy {a_n} podél levé hrany a členy {b_n} podél horní hrany imaginární nekonečné matice. Potom získáme všechny prvky této matice tak, že vždy vynásobíme odpovídající čísla ze záhlaví příslušného sloupce a řádku.

Členy konvoluce c_n pak najdeme sečtením podél diagonál.

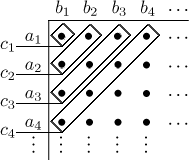
Jako příklad si spočítáme {1, −1, 2, −2, 3, −3,...} * {1, 2, 3, 4, 5, 6,...}:

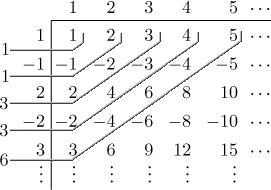
Takže

{1, −1, 2, −2, 3, −3,...} * {1, 2, 3, 4, 5, 6,...} = {1, 1, 3, 3, 6,...}

Z tohoto výsledku není zjevné, jak jde konvoluce dál, ale zdá se, že by členy výsledku mohly jít po dvou. Zkusil jsem udělat matici 10 krát 10 a vyšlo mi {1, 1, 3, 3, 6, 6, 10, 10, 15, 15,..}. Podezření, že čísla jdou po dvou, je teď ještě silnější, ale co je to vlastně za čísla? Jaká posloupnost jde 1, 3, 6, 10, 15,...? To se dá uhádnout, protože lidem, kteří dělají s posloupnostmi, tato čísla přijdou povědomá: Její n-tý člen je součet 1 + 2 +...+ n. Po 15 by tedy měl přijít její šestý člen, neboli 1 + 2 + 3 + 4 + 5 + 6 = 21. Ověřte to spočtením dalšího členu konvoluce. Máme tedy pěknou hypotézu, její důkaz ale nebude snadný, takže to necháme odborníkům.

Konvoluce není používána přímo při zkoumání posloupností jako takových, při sledování jejich vlastností. Odkazujeme proto na rozličné aplikace pro další vlastnosti konvoluce. Zde v Math Tutoru se konvoluce objevuje na dvou místech, jmenovitě když uvedeme násobení řad a také násobení mocninných řad; tam to hraje klíčovou roli.

Zpět na Teorie - Úvod