Základní vlastnosti

Zde se podíváme na omezenost a monotonii, dvě základní vlastnosti posloupností. Uvedeme příslušné definice, vysvětlíme je a ukážeme několik příkladů. Další jednoduché příklady jsou v následující sekci Důležité příklady, dva řešené příklady jsou v části Řešené příklady.

Omezenost

Posloupnost je omezená, jestliže můžeme omezit velikost všech jejích členů.

Definice.
Řekneme, že posloupnost {a_n} je omezená zdola, jestliže existuje číslo k (dolní mez) takové, že pro všechna n máme a_n ≥ k.
Řekneme, že posloupnost {a_n} je omezená shora, jestliže existuje číslo K (horní mez) takové, že pro všechna n máme a_n ≤ K.
Řekneme, že posloupnost {a_n} je omezená, jestliže je omezená shora i zdola.

Posloupnost {a_n} je tedy omezená, existují-li čísla k a K taková, že pro všechna n máme k ≤ a_n ≤ K.

Je důležité poznamenat, že slova "pro všechna n" znamenají "pro všechna n použitá k indexaci posloupnosti"; typicky to znamená pro všechna čísla n = 1,2,3,..., ale víme už, že se dá začít číslování i od jiného čísla než od jedničky.

Když se podíváme na graf posloupnosti, tak omezenost zdola znamená, že je možné nakreslit vodorovnou čáru tak, aby všechny body reprezentující členy posloupnosti byly nad touto čárou. Podobně omezenost shora je splněna, pokud všechny body dané posloupnosti zůstanou pod určitou vodorovnou přímkou; omezenost pak znamená, že členy posloupnosti je možné uzavřít mezi dvě vodorovné přímky.
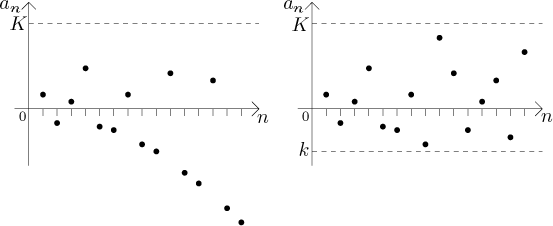
Na následujícím obrázku je levá posloupnost omezená shora, ale není omezená zdola a tudíž ani omezená. V daném obrázku vlastně je možné nakreslit vodorovnou čáru pod všemi body, ale máme na paměti, že obrázek ukazuje pouze začátek posloupnosti, která pokračuje doprava do nekonečna naznačeným způsobem; protože každý další člen se zdá poklesnout o konstantní hodnotu dolů, vypadá to, že ať už nakreslíme vodorovnou čáru kdekoliv, posloupnost dříve či později klesne pod ni.
Posloupnost vpravo je omezená, omezená shora i zdola.

Příklad: Uvažujme posloupnost a_n = (4 − 3n)/n², n = 1,2,3,...
Podíváme se na několik prvních členů; posloupnost začíná {1, −1/2, −5/9, −1/2, −11/25, −7/18, −17/49, −5/16, −23/81, −13/50,...}.

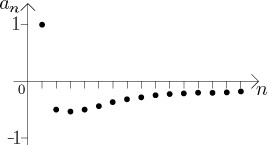
Z obrázku by se zdálo, že a_n ≤ 1 a a_n ≥ − 1. Pokud se nám to podaří dokázat, posloupnost bude potvrzena coby omezená. Pro důkaz jsme zvolili nejjednodušší způsob, uděláme to "z definice": Napíšeme nerovnosti, které chceme, aby podle definice platily, a pak je prozkoumáme, jestli opravdu fungují.

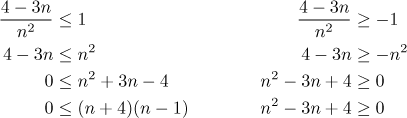
V posledním řádku je levá nerovnost pravdivá pro všechna n ≥ 1 a pravá nerovnost pro všechna n. Skončili jsme tedy s pravdivými tvrzeními, a protože jsme k nim došli ekvivalentními úpravami, můžeme obrátit proces a dostaneme, že i původní tvrzení o omezenosti byla pravdivá.

Poznámka:
Je zřejmé, že jakmile dostaneme nějakou horní či dolní mez, najdeme i mnoho dalších. V našem příkladě jsme použili −1 a 1, ale mohli jsme použít například −3/4 a 13. Obvykle je jednodušší použít pěknější čísla, kdybychom zkusili dokázat, že pro všechna n máme a_n ≥ −3/4, asi bychom se trochu víc zapotili.

Když nějakou posloupnost podezříváme, že je omezená, lze při důkazu často ušetřit čas tím, že raději zkoumáme její absolutní hodnotu. Například v našem posledním příkladě jsme mohli zkusit dokázat, že |a_n| ≤ 1 pro všechna n, což by prokázalo omezenost shora i zdola v jednom kroku. V tomto našem příkladě se to vlastně nezdá příliš jednodušší; nicméně jsou příklady, kde trik s absolutní hodnotou výrazně pomůže.

Narazili jsme tím vlastně na obecné tvrzení.

Fakt.
Posloupnost {a_n} je omezená právě tehdy, existuje-li číslo h splňující |a_n| ≤ h pro všechna n.

Důkaz: Pokud posloupnost splňuje tuto podmínku, pak zjevně -h ≤ a_n ≤ h pro všechna n a posloupnost je tedy omezená.
Na druhou stranu, pokud máme omezenou posloupnost, pak máme také nějakou horní a dolní mez z definice omezenosti, neboli jsou zde k a K splňující k ≤ a_n ≤ K pro všechna n. Definujme h = max(|k|,|K|). Pak -h ≤ k a K ≤ h, proto -h ≤ a_n ≤ h pro všechna n. To je přesně ta podmínka z Faktu.

Všimněte si, že omezenost se vlastně rozhoduje na "konci" posloupnosti. Konečná množina čísel má vždy své maximum a minimum, takže omezenost je možné zkazit pouze tím, že uvažujeme nekonečně mnoho čísel. Řečeno jinak, pokud z posloupnosti vyhodíme konečně mnoho členů (například její začátek, její omezenost se nezmění. Proto když zkoumáme omezenost, tak nás vlastně příliš nezajímá, kde jsme začali indexování; pokud to pomůže, klidně můžeme ignorovat několik prvních členů a brát v úvahu jen n > N pro nějaké vhodně zvolené N.

Následující dvě tvrzení by vám měla přijít přirozená: Pokud je posloupnost omezená, pak jsou všechny její podposloupnosti omezené. Pokud má posloupnost neomezenou podposloupnost, pak je sama neomezená.

Zde zadefinujeme, co to znamená, je-li posloupnost monotonní. Je to obecný pojem zahrnující pojmy rostoucí a klesající.

Definice.
Řekneme, že posloupnost {a_n} je rostoucí, jestliže pro všechna n platí a_n < a_n+1.
Řekneme, že posloupnost {a_n} je neklesající, jestliže pro všechna n platí a_n ≤ a_n+1.
Řekneme, že posloupnost {a_n} je klesající, jestliže pro všechna n platí a_n > a_n+1.
Řekneme, že posloupnost {a_n} je nerostoucí, jestliže pro všechna n platí a_n ≥ a_n+1.
Řekneme, že posloupnost {a_n} je monotonní, jestliže splňuje některou z těchto čtyř podmínek.

Abychom pochopili tyto definice, je třeba si uvědomit následující. Je-li dáno n, pak a_n reprezentuje určitý člen dané posloupnosti a a_n+1 je člen s indexem o jedničku větším, neboli je to přesně následující člen. Rostoucí tedy znamená, že pokud se podíváme na nějaký člen posloupnosti, pak ten následující musí být větší, a toto musí platit pro všechny takové následné dvojice. Protože definice rostoucí posloupnosti vyžaduje, aby toto splňovaly všechny dvojice, vyplývá z toho, že stačí jediný pár po sobě následujících bodů, který danou nerovnost nesplňuje, aby posloupnost již nebyla rostoucí. Podobně je tomu i pro ostatní pojmy z této definice.
U rostoucí posloupnosti tedy musí být každý člen větší než ten předchozí; u neklesající posloupnosti se vyžaduje, aby také rostla, ale je jí také povoleno, aby někdy (nebo třeba pořád) zústala stejná - jediné, co nesmí, je někde klesnout. Význam definic by měl být jasný, když se podíváte na následující čtyři typické příklady. Jsou ve stejném pořadí, v jakém byly v definici.

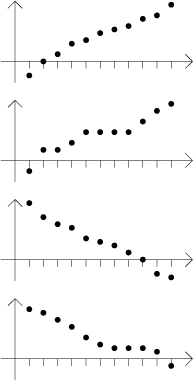
Mezi těmito pojmy existují určité vztahy. Rostoucí posloupnost je automaticky neklesající a klesající posloupnost je automaticky nerostoucí. Existují dokonce posloupnosti, které jsou zároveň neklesající a nerostoucí - jmenovitě konstantní posloupnosti. Na druhou stranu, rostoucí posloupnost nemůže být klesající a naopak.

Příklad: Uvažujme posloupnost z předchozího příkladu a_n = (4 − 3n)/n², n = 1,2,3,..., která, jak jsme už viděli, začíná
{1, −1/2, −5/9, −1/2, −11/25, −7/18, −17/49, −5/16, −23/81, −13/50,...}.

Co je možné říct o monotonii této posloupnosti?
Protože druhý člen je menší než první, a₁ = 1 > −1/2 = a₂, posloupnost nemůže být rostoucí ani neklesající (ona totiž klesla, když šla od a₁ k a₂, viz poznámka po definici). Mohla by být klesající nebo nerostoucí? Nemohla, protože roste přinejmenším na jednom místě, máme a₃ = −5/9 < −1/2 = a₄. Závěr: Posloupnost není monotonní.

Všimněte si, že když ignorujeme první dva členy a uvažujeme posloupnost a_n = (4 − 3n)/n², n = 3,4,5,..., která začíná {−5/9, −1/2, −11/25, −7/18, −17/49, −5/16, −23/81, −13/50,...}, dostaneme rostoucí posloupnost. Na obrázku se to zdá fungovat, ale obrázek samozřejmě není důkaz - už proto, že z posloupnosti vidíme jen kousek. K pokročilejším metodám zkoumání monotonie se dostaneme později (viz Posloupnosti a funkce v části Teorie - Limita a Přehled metod - Základní vlastnosti), tady to prostě zkusíme z definice. Začneme nerovností, o které doufáme, že platí, a prozkoumáme ji.

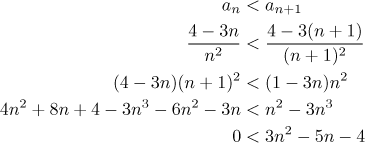
Poslední nerovnost platí pro všechna n = 3,4,5,... (platí také pro všechna n < −1, ale to nás nezajímá). Protože jsme používali ekvivalentní operace, platí také první nerovnost, takže ona zkrácená posloupnost je vskutku rostoucí, proto také monotonní.
Všimněte si, jak jsme dosazovali za a_n+1. Tady začátečníci s oblibou dělají chyby, ale jakmile jednou pochopíte, jak to funguje, mělo by to být snadné. Máme a_n = (4 − 3n)/n². Jak vypočítáte a₁₃? Dáte 13 namísto všech n ve vzorci. Jak vypočítáte a_k? Stejným způsobem, místo všech n dáte ve vzorci k. Teď si jen představte, že máte k = n + 1.

Viděli jsme, že na rozdíl od omezenosti se monotonie dá změnit tím, že z posloupnosti odebereme či do ní přidáme členy.

V jednom směru máme nicméně něco positivního: Pokud je posloupnost monotonní, pak jsou všechny její podposloupnosti monotonní. Když si nakreslíte pár obrázků, mělo by vám být jasné, že toto opravdu platí. Všimněte si, že je dokonce zachován i "směr", podposloupnost posloupnosti, která jde "nahoru", půjde také "nahoru". Občas se ale může změnit konkrétní typ.

Příklad: Uvažujme posloupnost definovanou pro n = 0,1,2,... následovně:

Co to znamená? Pokud je n sudé, pak a_n = n/2, a pokud je n liché, pak a_n = (n − 1)/2. Posloupnost začíná {0, 0, 1, 1, 2, 2, 3, 3, 4, 4, 5, 5,...}. Je tedy monotonní, jmenovitě neklesající. Pokud z ní vytvoříme podposloupnost tak, že vybereme každý druhý člen, dostaneme posloupnost {0, 1, 2, 3, 4, 5,...}. Jak říkalo to tvrzení, i tato posloupnost je monotonní a jde nahoru. Teď se ovšem zlepšila "kvalita" toho růstu, posloupnost není jen neklesající, je dokonce rostoucí.

Pokud začneme s posloupností, která není monotonní, a vybereme z ní podposloupnost, pak situace může zůstat stejná, nebo se může zlepšit. Pokud například vybereme každý druhý člen z alternující posloupnosti {1, −1, 1, −1, 1,...}, která není monotonní (viz následující sekce Důležité příklady), dostaneme monotonní posloupnost {−1, −1, −1, −1,...}.

Monotonie někdy pomůže při zkoumání konvergence, viz Základní vlastnosti v části Teorie - Limita.

Důležitá poznámka.
Bohužel, terminologie, kterou jsme uvedli výše, není obecně uznávaná. Dává jí přednost mnoho autorů, ale mnoho jich zase upřednostňuje terminologii konkurenční. Namísto pojmů (v pořadí jako jsme je zavedli)
rostoucí, neklesající, klesající, nerostoucí
používají
striktně rostoucí, rostoucí, striktně klesající, klesající.
Slovo monotonie používají stejně jako my, ale pro první a třetí pojem také používají společného pojmu striktní monotonie.

Tento zmatek je nešťastný, ale naštěstí z něho není moc velký průšvih. Ve větách se obvykle vyžaduje monotonie, v kterémžto pojmu se obě školy shodují. Samozřejmě jako obvykle, učitel, ke kterému chodíte na přednášky, má vždycky pravdu, takže se držte jeho terminologie. Zde se budeme držet té, kterou jsem definoval, už proto, že se jí držel můj profesor, a tak ji posílám dál.
Musíme nicméně čtenáře varovat, že je okamžik, kdy se tyto školy střetávají: ve větách, které dávají do souvislosti monotonii a derivaci. Když o tom čtete, dobře se podívejte, jaká terminologie je použita.

Důležité příklady
Zpět na Teorie - Úvod