Definice.
Uvažujme dvě řady,
![]() ak
ak![]() bk.
bk.
Definujeme jejich součet jako řadu
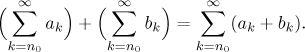
Uvažujme řadu
![]() ak
ak
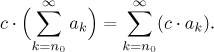
V této sekci se podíváme na některé vlastnosti řad, zejména uvidíme, co se změní, když přejdeme od konečných součtů k nekonečným. Začneme operacemi, pak se podíváme na vybrané řady a přerovnání a poté se podíváme na základní a nejdůležitejší fakta o konvergenci. Nakonec probereme řady s nezápornými členy.
Když v matematice pracujeme s objekty, tak je rádi spojujeme dohromady, což děláme pomocí rozličných operací. Tuto sekci začneme definováním dvou nejpopulárnějších operací s řadami.
Definice.
Uvažujme dvě řady,a ak
bk.
Definujeme jejich součet jako řadu
Uvažujme řadu
a reálné číslo c. Součin čísla a řady definujeme jako ak
Jak vidíte, definovali jsme tyto operace tak, aby pracovaly "člen po členu", neboli na řadu působíme tak, že působíme na každý její člen. Tento způsob je v matematice populární a obvykle dává dobré výsledky. Platí to i zde. Všimněte si, že abychom byli schopni sečíst dvě řady, musí být indexovány stejným způsobem. V mnoha případech to je jen technický problém, viz změna indexace v předchozí sekci. V definici jsme pomocí oněch dvou operací vytvořili nové řady, teď si ukážeme, že se chovají rozumně.
Věta.
(i) Jestliže řadakonverguje, pak pro každé reálné číslo c konverguje i řada ak
a (c ak)
(ii) Jestliže řady
a ak
obě konvergují, pak také řada bk
konverguje a (ak + bk)
Protože se odčítání dá přepsat jako sčítání, tato věta také funguje pro odčítání. Má dva důležité aspekty.
1. Často dokážeme lépe ocenit význam výrazů se sumami, když si je rozepíšeme "dlouhým způsobem", v tomto případě jako nekonečné součty. Přepíšeme teď obě tvrzení z věty a pro jednoduchost předpokládáme, že indexy začínají v 1.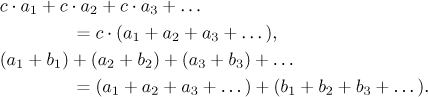
Vidíme, že první tvrzení je vlastně jen zobecnění distributivního zákona z konečných sum na nekonečné. Druhé tvrzení je speciální verze komutativního zákona. Později uvidíme (viz konec sekce Absolutní konvergence), že s komutativním zákonem je u nekonečných součtů problém; to, co tu máme, je asi nejlepší, co jde dostat.
2. Na rozdíl od podobných zákonů pro konečné součty jsou tyto dvě rovnosti "jednosměrné" a podmínečné. Dá se v nich jít jen zprava doleva, to platí obzvláště o části (ii). Pokud víme, že výraz na pravé straně má smysl (ony dvě řady konvergují), pak a jen pak se můžeme přesunout doleva a sečíst je v jednu řadu. Jinými slovy, rovnosti v oné větě fungují jen někdy, například pokud jsou splněny podmínky specifikované ve větě. Když tedy máme řadu a chceme ji rozdělit na dvě, pak jsme v nebezpečné situaci, protože to je přesně něco, co nám věta neumožňuje (snažíme se jít zleva doprava). Když vezmeme řadu a napíšeme ji jako součet dvou, pak ta rovnost není opravdu rovnost, je to "podmínečná" rovnost ve smyslu, že ve chvíli jejího napsání ještě nevíme, jestli je pravdivá. Musíme se podívat na vzniklou pravou stranu, a pokud tam věci dopadnou dobře (ony dvě řady konvergují), pak teprve víme, že je to celé v pořádku a ona rovnost je pravdivá; jinak můžeme dělat něco velmi špatného.
Schválně se podívejte na následující dva příklady:
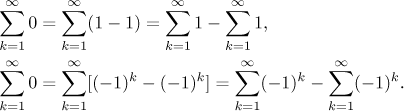
V obou případech máme na levé straně krásné konvergentní řady (viz předchozí sekce), ale nebyli jsme opatrní a rozdělili tyto dvě řady dosti nemoudře. V prvním případě jsme dostali dvě divergentní řady a výraz napravo je neurčitý, nekonečno mínus nekonečno. V druhém případě je to dokonce horší, protože ony dvě řady napravo divergují nejhorším možným způsobem (oscilace) a dokonce ani nelze říct, jaký typ výrazu napravo máme.
První rovnost (i) je poněkud hezčí, jediný opravdický problém nastane pro nulové
c, jinak je také možno jít zleva doprava. Pokud totiž víme, že řada
nalevo konverguje a c není nula, pak podle věty je možno ji vynásobit
číslem
Poznámka: Větu lze formulovat obecněji. Jestliže má výraz na pravé straně smysl, pak je dotyčná rovnost pravdivá.
Pro část (i) proto také dostaneme rovnost, jestliže původní řada je nekonečno nebo mínus nekonečno a c není nulové (připomeňme, že nula krát nekonečno je neurčitý výraz, problémy působí i zde).
Pro část (ii) víme, že rovnost je pravdivá, pokud výraz na pravé straně (součet dvou řad) má smysl, což znamená, že tam mohou být dvě reálná čísla, nebo jedno reálné číslo a jedno (mínus) nekonečno, nebo dvě nekonečna nebo dvě mínus nekonečna. Také o sčítání konvergentní řady a "špatně" divergentní řady (oscilující řady, která nedává ani (mínus) nekonečno) se dá říct, že "má smysl", výsledkem je opět divergující řada. Sčítání konvergentní a divergentní řady proto vždy funguje, ať už je ta divergence jakákoliv, výsledná řada diverguje stejným způsobem jako onen divergentní sčítanec.
Fakt.
Jestliže řadakonverguje a řada ak
diverguje, pak řada bk
diverguje. (ak + bk)
Můžeme totiž vyjádřit
![]() bk
bk![]() (ak + bk)
(ak + bk)![]() ak,
ak,![]() bk
bk
Jaké jsou případy, kdy tato rovnost neplatí? Příklad výše ukazuje ty nejtypičtější, kdy pravá strana dává nekonečno mínus nekonečno nebo nějakou kombinaci "špatných divergencí". Pak nevíme nic o tom, co se stane s řadou nalevo, může být konvergentní (například když se dvě nekonečna navzájem vykrátí), "pěkně" divergentní nebo "špatně" divergentní.
Můžeme také narazit s asociativním zákonem. Obecně vzato, když do řady
zavedeme nějaké sdružování pomocí závorek, můžeme se dostat do potíží.
Připomeňme si například naši oblíbenou alternující řadu
(1 − 1 + 1) + (−1 + 1 − 1) + ... = 1 − 1 + 1 − ...,
(1 − 1) + (1 − 1) + (1 − 1) + ... = 0 + 0 + 0 + ... = 0,
1 − (1 − 1) − (1 − 1) − (1 − 1) − ... = 1 − 0 − 0 − 0 − ... = 1.
Jak vidíte, prostou aplikací asociativního zákona různými způsoby jsme dostali (vycházejíce ze stejné řady) řadu divergentní a dvě řady konvergentní, ale každá jde jinam. Je tedy jasné, že pro nekonečné součty už "asociativní zákon" není zákonem. Příští tvrzení naštěstí říká, že pokud se držíme konvergentních řad, měli bychom být v pohodě. Nenechte se vyděsit poněkud drsnějším značením, vyjádřit asociativní zákon pořádně není snadné.
Věta (asociativní zákon).
Předpokládejme, že řadakonverguje. Pak pro každou rostoucí posloupnost ak
k1 < k2 < k3 < ... splňujícín0 = k1 také řadakonverguje a
V dlouhém rozpisu:
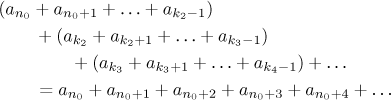
Zase to funguje jen ve směru podaném ve větě, tedy zprava doleva v rovnici. Naopak to obecně platit nemusí, klidně se může stát, že ta uzávorkovaná řada nalevo konverguje, ale ta napravo ne (už jsme to viděli výše).
Měli bychom poznamenat, že existuje i další užitečná situace, kdy můžeme použít pro řady asociativní zákon. Pokud mají všechny členy v řadě stejné znaménko (například pokud jsou všechny členy nezáporné), pak je rovnost v této větě vždy pravdivá, a to dokonce v obou směrech (viz níže).
Násobení.
Přirozený přístup je rozšířit násobení, jak se dělá pro součiny konečných
součtů. Tam používáme metodu "každý člen z první části krát každý člen z
druhé části" a tyto součiny se pak posčítají. U řad toto vede na nekonečně
mnoho malých součinů typu
Definice.
Uvažujme řadya ak
Definujeme jejich součin jako řadu bk.
Rozepsáno dlouhým způsobem,
Říká se tomu také Cauchyho součin. Ačkoliv je právě toto přirozený součin, má jednu nepříjemnou vlastnost: Může se stát, že když vynásobíme dvě konvergentní řady, tak dostaneme řadu, která diverguje! Pokud chceme zajistit konvergenci součinu, je třeba požadovat více, například že jedna z těch dvou řad je absolutně konvergentní. Pak se tento součin chová přesně tak, jak by se čekalo od "rozumného" součinu, jmenovitě
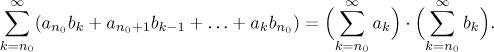
Cauchyho součin potom také splňuje asociativní a komutatovní zákon a rovněž distributivní zákon. Všechny tyto zákony jsou "podmínečné": Jestliže má výsledek operace smysl, pak je tato operace platná.
Jedno zajímavé pozorování: Máme řadu se členy
ak a řadu se členy
bk. Jaké jsou členy jejich součinu? Odpověď: Je to
konvoluce
posloupností
Poznámka: Dá se také uvažovat o jiném přirozeném způsobu násobení dvou řad, jmenovitě násobení "člen po členu". Výsledná řada by byla prostě součtem členů akbk. Takové násobení je opravdu možné a také splňuje obvyklá pravidla pro násobení (komutativitu, asociativitu). Součin po členech dvou konvergentních řad je zase konvergentní řada (zde máme zlepšení v porovnání s Cauchyho součinem); nicméně jeho součet nemá nic společného se součty jednotlivých řad v součinu. Jinými slovy, pokud vynásobíme řadu se součtem řekněme 5 s řadou se součtem 2, pak téměř jistě nedostaneme pomocí součinu po členech řadu se součtem 10. Už toto ukazuje, že pojem součinu po členech není příliš vhodný pro naše aplikace a proto jej budeme víceméně ignorovat (stejně jako většina autorů).
Když máme řadu, rádi bychom někdy sečetli jen některé její členy (jakási "podřada" ve smyslu podobném "podposloupnosti"). Značení se dělá tak, že si vybereme indexy čísel, která nás zajímají.
Definice.
Uvažujme řaduak. Nechť A je podmnožina množiny
{n0, n0 + 1, n0 + 2, n0 + 3,...}, označme její členy jakoA = {k1 < k2 < k3 <...}. Pak definujeme součet přes A jako
Takové řadě se také říká vybraná řada.
Když přejdeme k podmnožině členů řady, můžeme tím podstatně změnit její
chování. Uvažujme například alternující řadu ![]() . Víme, že kvůli oscilaci
diverguje nejhorším možným způsobem. Když vezmeme jako A všechna sudá
přirozená čísla, dostaneme řadu, která sčítá členy
. Víme, že kvůli oscilaci
diverguje nejhorším možným způsobem. Když vezmeme jako A všechna sudá
přirozená čísla, dostaneme řadu, která sčítá členy
Samozřejmě existuje případ, kdy tímto způsobem vždy dostaneme konvergentní řadu, jmenovitě když je A konečná množina. Když si totiž z řady vybereme konečný počet členů k sečtení, dostaneme konečný součet, který vždy funguje. Existuje ještě jiný způsob, jak zaručit, že přechod na vybranou řadu bude fungovat, jmenovitě silnější (lepší a přísnější) pojem konvergence. Na to se musíte podívat do sekce Absolutní konvergence.
V zásadě totéž platí pro další trik, který se s řadou dá udělat. Už jsme výše naznačili, že mohou být problémy s komutativním zákonem. Jak se komutativní zákon vyjádří pro řady? Máme nějaká čísla a pořadí, ve kterém jsou sčítána, je určeno jejich indexy, jdeme od menšího k většímu. Pokud tedy chceme zamíchat čísla a sečíst je v jiném pořadí (přerovnat je), uděláme to změnou indexace. Připomeňme, že když máme množinu celých čísel uvažovanou s určitým pořadím a chceme změnit jejich pořadí, říkáme tomu permutace. Matematicky můžeme takovou permutaci vyjádřit jako bijekci P na oné množině.
Předpokládejme například, že máme řadu a indexování jejích členů jde
a1, a2, a3,
a4,..., řekněme že
a3 = 13. Když tuto řadu sčítáme, tak abychom
viděli třetí číslo, vezmeme
Teď si představme, že tuto řadu chceme přerovnat tak, aby se tato konkrétní
13 brala jako pátý člen. Pak uvažujeme permitaci P takovou, že
Definice.
Uvažujme řaduJejím přerovnáním rozumíme libovolnou řadu ve tvaru ak.
kde P je nějaká permutace množiny aP(k),
{n0, n0 + 1, n0 + 2, n0 + 3,...}.
Zase jsme ve veselé situaci, že dokonce i konvergentní řada může být
přerovnána v řadu divergentní. Všimněme si, že když je P konstantní
s výjimkou konečně mnoha členů (takže děláme jen konečně mnoho změn v dané
řadě), pak je určitý index K takový, že se všechny změnu udály před
tímto K (jinak řečeno,
Skutečný problém s komutativním zákonem tedy nastává v situacích, kdy potřebujeme přesunout nekonečně mnoho členů. Zde zase silně pomůže absolutní konvergence.
Už jsme v této sekci viděli, jak důležitá konvergence je. Zde si o ní ukážeme několik základních výsledků.
Věta.
Uvažujme řadunechť ak,
n1 > n0.
konverguje tehdy a jen tehdy pokud ak
konverguje; pak také
Dá se říci více: Dvě řady, které sdílejí členy a liší se jen tím, kde začínají, se chovají přesně stejně. Jestliže jedna dá nekonečno, tak i ta druhá. Jestliže jedna "špatně" diverguje (s oscilací), tak i ta druhá. Také ta rovnost je pravdivá, "kdykoliv má smysl." Protože konečný součet napravo je vždy reálné číslo, tak má pravá strana smysl pro řady, které jsou konvergentní, a také pro řady se součtem nekonečno či mínus nekonečno.
Tato věta má dva užitečné důsledky. Za prvé vidíme, že když pracujeme s
řadou, tak si můžeme s konečnými úseky pohrát stranou, kdykoliv se nám to hodí.
Co je důležitější, vidíme, že se chování řady rozhoduje "na jejím konci,"
její začátek to neovlivňuje. Když pracujeme s řadami, často nás víc než její
součet (pokud vůbec nějaký je) zajímá, jestli konverguje. Pak nepotřebujeme
vědět, kde indexace začíná, můžeme začít, kde se nám zachce, takže se to
stává irelevantním. To silně zjednodušuje situaci a také se to odráží ve
značení. Když vyšetřujeme konvergenci řady, tak nepoužíváme plné značení
včetně specifikace indexace, prostě jen píšeme
Teď se na konvergenci podíváme blíže.
Věta (nutná podmínka konvergence).
Jestliže řada∑ ak konverguje, pak nutně posloupnost{ak} konverguje k 0.
Jak název napovídá, tato věta je jen implikace, takže jsou i divergentní řady, jejichž individuální členy jdou k 0. Můžeme se na to také podívat v opačném směru. Tato věta říká, že pokud čísla ak nejdou k nule, pak je odpovídající řada nutně divergentní. To je někdy užitečné jako nástroj k testování konvergence, ale jen zřídka, protože ty opravdu zajímavé řady jsou ty, jejichž členy jdou (coby jednotlivci) k nule. Když z nich pak uděláme řadu, tak může být konvergentní i divergentní. Takové řady jsou vlastně ty opravdu zajímavé, protože u nich je dělící čára mezi konvergencí a divergencí mnohem jemnější.
Všimněte si, že čísla ak zde hrají dvě rozdílné
role, coby jednotlivci (když tvoří posloupnost
Připomeňme, že při teoretické práci někdy pomůže fakt, že posloupnost konverguje tehdy a jen tehdy, když je Cauchyovská (viz Základní vlastnosti v části Posloupnosti - Teorie - Limita). Když to aplikujeme na částečné součty řad, dostaneme následující užitečné kritérium.
Věta (Cauchy-Bolzano).
Uvažujme řadu∑ ak. Tato řada konverguje tehdy a jen tehdy, když pro každéε > 0 existuje přirozené číslo N takové, že pro všechnam > n ≥ N máme
Jeden z důvodů, proč se zkoumání konvergence může zkomplikovat, je to, že se řada může chovat mnoha různými způsoby. S některými řadami se ale pracuje lépe.
Představte si, že daná řada má všechny členy nezáporné. To znamená, že jak
přičítáme její členy, postupné součty se mohou pouze zvyšovat, přinejhorším
zůstanou stejné. Jinými slovy, částečné součty tvoří neklesající posloupnost.
Formálně je to snadné, z podmínky
Neklesající posloupnosti buď konvergují nebo jdou do nekonečna (viz Základní vlastnosti v části Posloupnosti - Teorie - Limita), dostaneme tedy následující tvrzení.
Věta.
Uvažujme řadu∑ ak. Jestližeak ≥ 0 pro všechna k, pak buď∑ ak konverguje nebo∑ ak = ∞.
Už jsme se zmínili, že řady s nezápornými členy se chovají mnohem lépe, při povídání o asociativitě výše, teď to zformulujeme přesně a jako bonus přidáme tvrzení o přerovnání.
Věta.
Uvažujme řadutakovou, že ak
ak ≥ 0 pro všechna k.
(i) Pro libovolnou rostoucí posloupnostk1 < k2 < k3 < ... splňujícín0 = k1 platí následující:
(ii) Pro každé přerovnání
platí následující: aP(k)
aP(k) =
ak.
Díky předchozí Větě jsou všechny součty v oněch dvou rovnostech výše buď reálná čísla (řada konverguje) nebo nekonečno, a ty rovnosti jsou platné ve všech případech. Takže pokud se v určité rovnosti jedna z řad posčítá do nekonečna, pak to musí platit i o té na druhé straně a naopak; podobně konvergence přechází z jedné strany na druhou. Práce s řadami s nezápornými členy je tudíž velice příjemná, totéž je samozřejmě pravda o řadách s nekladnými členy.
Asi největší výhodou řad s nezápornými členy je, že se jejich konvergence zkoumá relativně snadno. Ve skutečnosti se dá většina testů konvergence aplikovat právě jen na takovéto řady. Je jasné, že když jsou všechna čísla v řadě záporná (či nulová), tak vždycky můžeme to mínus vytknout z řady a dostaneme řadu s nezápornými členy, takže všechno, co jsme tu říkali, platí také (se zjevnými modifikacemi) pro řady s nekladnými členy. Jediný problémový případ je tedy ten, kdy mají členy v řadě rozličná znaménka, což není žádný překvapovák, už jsme naznačili, že oscilační divergence je ta nejhorší.