Posloupnosti a funkce

Když je posloupnost dána vzorcem (explicitní definicí), tentýž vzorec obvykle také definuje funkci. Je opravdu jen málo formulek, které by fungovaly pro přirozená čísla, ale ne pro reálná čísla mezi nimi. Jedním takovým kandidátem je faktoriál n!, který size lze rozšířit na reálná čísla pomocí funkce Gama, ale není to dostatečně známá funkce na to, aby to bylo praktické řešení. Snad nejdůležitější ale je, že mocniny se zápornými bázemi jako (−1)ⁿ prostě nelze rozšířit na funkce nad reálnými čísly.

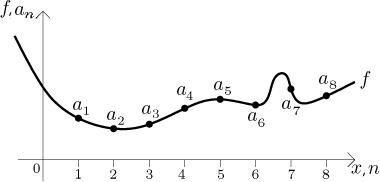
Zde je tedy typická situace. Máme funkci f (x) definovanou na nějakém intervalu (K,∞) a stejný vzorec je použit v definici posloupnosti: a_n = f (n) pro celá čísla n > K. To znamená, že vlastně vybíráme body z grafu f a z nich tvoříme posloupnost.

Jaká je souvislost mezi vlastnostmi funkce a vlastnostmi posloupnosti?

Protože posloupnost je částí funkce, zdědí relevantní vlastnosti:

Věta.
Nechť f (x) je funkce definovaná na nějakém intervalu (K,∞), definujme posloupnost a_n = f (n) pro celá čísla n > K.
• Jestliže je f omezená v nějakém smyslu, pak je i posloupnost {a_n} omezená ve stejném smyslu.
• Jestliže je f monotonní, pak je i posloupnost {a_n} monotonní (ve stejném směru).
• Jestliže má f limitu L pro x jdoucí do nekonečna, pak má i posloupnost {a_n} limitu L.

Když proto zkoumáme posloupnost, můžeme zkusit zkoumat místo ní relevantní funkci pomocí silných nástrojů, které pro funkce máme, a pokud dostaneme nějaké "pozitivní" výsledky, budou platit i pro danou posloupnost.

Všimněte si, že tato procedura pouze platí pro "pozitivní" poznatky. Pokud by se ukázalo, že funkce není omezená, není monotonní či nemá limitu ("záporné" poznatky), pak tento závěr nelze přenést na posloupnost. Ekvivalentně řečeno, implikace ve větě obecně neplatí v opačném směru. Může se stát, že posloupnost {a_n} má různé pěkné vlastnosti, ale funkce f z nich nemá žádnou. Důvod je jednoduchý: Protože posloupnost zastupuje jen malou část celé funkce, znalost chování posloupnosti nám nedá žádnou informaci o tom, co se děje s funkcí mezi body posloupnosti.

Jako příklad si uvedeme funkci f (x) = x⋅sin(πx) a posloupnost a_n = n⋅sin(πn).

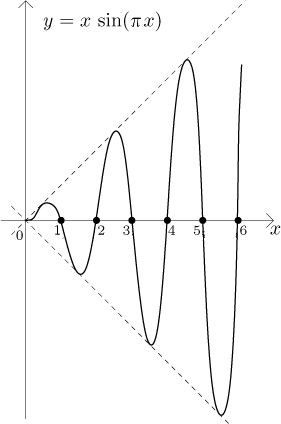
Vidíme, že posloupnost vlastně jde {0, 0, 0, 0,...}, neboli je to konstantní posloupnost. Jako taková je monotonní (zároveň nerostoucí a neklesající), omezená a konvergentní (k nule). Na druhou stranu, funkce f není omezená v žádném smyslu, není monotonní a nemá limitu v nekonečnu.

Co to znamená pro naše zkoumání posloupností? Když (jestli) zkusíme namísto posloupnosti zkoumat příslušnou funkci a dostaneme nějaký "pozitivní" výsledek, tak také platí podle věty i pro danou posloupnost. Na druhou stranu "negativní" výsledky (funkce nemá v nekonečnu limitu, není rostoucí atd) se nepřenášejí automaticky na danou posloupnost. V takovém případě musíme ke zkoumání posloupnosti použít jiné nástroje, přístup skrze funkce nepomohl.

Příklad: Ukážeme, že posloupnost a_n = (n − 1)/n je rostoucí.

Řešení: Budeme místo posloupnosti zkoumat odpovídající funkci f (x) = (x − 1)/x. Je definována na (0,∞), což zahrnuje všechna přirozená čísla. Derivace je f ′(x) = 1/x². Protože je derivace vždy kladná, je následně funkce f rostoucí na (0,∞) a proto je také daná posloupnost rostoucí.

L'Hospitalovo pravidlo
Zpět na Teorie - Limita