Gama a Beta funkce

Definice.
Pro kladné x definujeme Gama funkci předpisem

Tento integrál není lehké obecně spočítat, proto nejprve prozkoumáme Gama funkci v důležitých bodech. Začneme s x = 1:

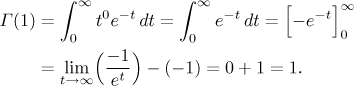
Teď se podíváme na hodnotu v x = 1/2:

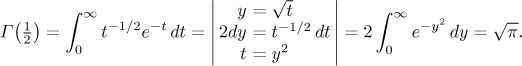
Ten poslední integrál nelze spočítat pomocí primitivní funkce (viz poznámka o Newtonovské integrabilitě). Tento určitý integrál je ale velmi důležitý (například v pravděpodobnosti), takže byl nalezen trik na jeho spočítání.

K nalezení hodnoty Gama funkce v dalších bodech odvodíme zajímavou identitu pomocí integrace per partes:

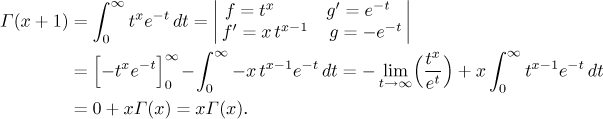
Limita se počítá několikanásobným použitím l'Hospitalova pravidla. Vidíme, že pro kladné x máme

Pokud toto aplikujeme na přirozené číslo n, dostaneme

Vidíme tedy, že Gama funkce je zobecněním faktoriálu. Dá se ukázat, že limita Gama funkce v bodě 0 zprava je nekonečná, takže tato funkce vypadá nějak takto:

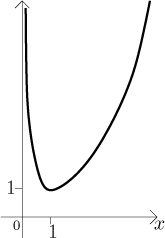
Protože hodnota Gama funkce v přirozených číslech je dána faktoriálem, plyne z toho, že utíká do nekonečna dokonce rychleji než exponenciály.

Pomocí substituce u = 1 − t lehce nahlédneme, že

K výpočtu Beta funkce se obvykle používají Gama funkce. Abychom našli jejich vzájemný vztah, je třeba provést docela komplikovaný výpočet zahrnující trikovou transformaci proměnných (z kartézských na trikové polární) v dvojném integrálu. To přesahuje rozsah této sekce, ale pro úplnost to zde uvedeme:

Takže

Více o objemu
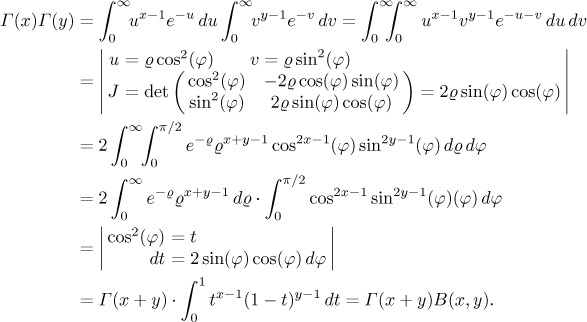
Zpět na Teorie - Aplikace