Příklad: Najděte následující limitu (pokud existuje)

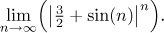
Řešení: Co se stane, když dosadíme nekonečno? Dostaneme (N + 3/2)^∞ = N^∞. Tento výraz se vyskytuje v algebře N jako neurčitý výraz; znamená to, že se na něj musíme podívat blíže.

Co se děje, když jde n do nekonečna? Sinus osciluje mezi −1 a 1, takže celá závorka osciluje mezi 1/2 a 5/2 (absolutní hodnoty tedy není třeba). Protože sinus je opakovaně téměř roven −1 a 1 znovu a znovu až do nekonečna, vyplývá z toho, že 3/2 + sin(n) se opakovaně blíží 1/2 a 5/2 znovu a znovu jak n jde do nekonečna. Daná posloupnost má tedy podposloupnost, která je téměř jako (1/2)ⁿ, a také má podposloupnost, lkterá je téměř jako (5/2)ⁿ. Když si teď připomeneme geometrickou posloupnost, víme, že (1/2)ⁿ→0 a (5/2)ⁿ→∞. To naznačuje, že máme dvě podposloupnosti, každá konvergující někam jinam, což by znamenalo, že celá daná posloupnost nemá limitu.

Jak to ale dokážeme korektně? Nemáme {(1/2)ⁿ} ani {(5/2)ⁿ}, máme "téměř (1/2)ⁿ" a "téměř (5/2)ⁿ" a měli bychom už vědět, že "téměř" může být dost nebezpečné, když dojde na limitu, zvlášť když se ono "téměř" umocňuje na velkou mocninu.

Asi nejjednosdušší je použít to, že se sin(n) přibližuje znovu a znovu libovolně blízko k −1 a 1 (viz Důležité příklady v části Teorie - Limita). Když si vybereme malou toleranci, sinus se nekonečně mnoho krát dostane v mezích této tolerance od −1 a od 1. Můžeme napríklad zvolit 1/4 jako toleranci. Pak existuje nekonečně mnoho n, pro které sin(n) < −3/4, a nekonečně mnoho n, pro které sin(n) > 3/4.

Nejprve tedy uvažujme podposloupnost přirozených čísel sestávající se z n splňujících sin(n) < −3/4. Pro tuto podposloupnost máme také (sin(n) + 3/2) < 3/4 a proto

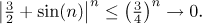
(V tomto srovnání jsme uvažovali pouze n z této konkrétní podposloupnosti). Podle Věty o sevření tedy tato konkrétní podposloupnost konverguje k nule.

Podobně když teď uvažujeme podposloupnost určenou těmi n, pro které sin(n) > 3/4, dostaneme (sin(n) + 3/2) > 2 a tudíž

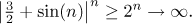
Proto tato konkrétní podposloupnost jde do nekonečna. Protože daná posloupnost (3/2 + sin(n))ⁿ má dvě podposloupnosti, které mají rozdílné limity, celá posloupnost nemá limitu (viz Teorie - Limita - Základní vlastnosti).

Poznámka: Abychom lépe ocenili, jak je toto řešení delikátní, podíváme se na následující příklad:

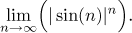
Nejprve se musíme zeptat, jestli to má vůbec smysl. Aby měla obecná mocnina smysl, musíme zajistit, že je báze kladná. Absolutní hodnota zabrání záporným číslům, aby se objevily, ale co nula? Víme, že sinus je roven nule pouze v celých násobcích π, ale je jen jeden z nich, který dává celé číslo, jmenovitě nula. Všechny ostatní násobky pí jsou iracionální čísla, z čehož vyplývá, že dokud je n přirozené číslo, sin(n) nemůže být nula. Výborně.

Víme tedy, že posloupnost má smysl, jak je to s jeho limitou? Čísla |sin(n)| oscilují mezi 0 a 1, takže když je umocníme na velké číslo, začnou se dít věci. Když je n opravdu opravdu veliké a |sin(n)| je o dost menší než 1, pak je výsledná mocnina skoro nula. Víme například, že (7/8)^∞ = 0, takže všechna n, pro které |sin(n)| < 7/8 a která jsou dost velká, dají nakonec velice malou mocninu. Můžeme tedy udělat první pozorovnání:

Když se podíváme na n, pro které |sin(n)| < 7/8, dostaneme podposloupnost konvergující k nule. Všimněte si, že většina přirozených čísel je v této podposloupnosti, ale je nekonečně mnoho n, která tam nejsou, pro které je |sin(n)| blíže k 1 než 7/8. Co se tedy stane s těmito n "navíc"? Jsou dvě možnosti. Jedna je, že také tyto n, když se stanou velkými, udělají |sin(n)|ⁿ libovolně malým. Celá posloupnost by pak šla k nule.

Je nicméně také možné, že tyto "odpadlé" n tvoří podposlouponost {|sin(n)|ⁿ}, která nekonverguje k nule, a potom by - jako v předchozím případě - daná posloupnost neměla limitu. Která alternativa je správná?

Můžeme zkusit zahrnout více n v naší "nulové podposloupnosti" tím, že použijeme menší toleranci. To ale nepomůže. Například množina n splňující |sin(n)| < 11/12 je rozhodně větší, než ta použitá s 7/8, ale stejně je pořád nekonečně mnoho n, které do ní nejsou zahrnuty. Podobně, pro libovolné q < 1 vždy existuje nekonečně mnoho n, které udělají sinus větší než q a tak nejsou zahrnuty v části, která jde k nule. Toto ukazuje, že zmenšením tolerance nemůžeme ukázat, že daná posloupnost konverguje k nule.

Co když se pokusíme použít ty n s velkým sinem ke zformování druhé podposloupnosti, která by měla jinou limitu? Nedokážeme to, protože pro ně nemáme dobrý dolní odhad. Zkusme třeba uvažovat množinu n splňujících |sin(n)| > 7/8. Dostaneme pak srovnání

|sin(n)|ⁿ > (7/8)ⁿ→0.

Srovnání tedy říká, že jestliže podposloupnost těchto n konverguje, pak ta výsledná limita je 0 či více, což vůbec nepomůže. Toto ukazuje rozdíl mezi dvěma příklady, které zde zkoumáme. V prvním příkladě jsme dokázali oddělit základ od 1 správným směrem. Nejprve jsme našli pro sinus horní odhad 3/4, a 3/4 je menší než 1. Protože (3/4)^∞ = 0, tento odhad přinutil příslušnou podposloupnost jít k nule. V druhém příkladě jsme to mohli udělat také.

V prvním příkladě jsme pak našli dolní odhad pro sinovou bázi pomocí 2, což je větší než 1, a protože 2^∞ = ∞, srovnání přinutilo tuto podposloupnost jít jinam než k nule. A to je přesně ten rozdíl, v druhém příkladě nejsme schopni najít dolní odhad pro |sin(n)| číslem větším než 1!

Vraťme se k druhému příkladu. Máme tu zlobící nekonečnou množinu n pro která je |sin(n)| téměř 1, takže nevíme, jak přinutit |sin(n)|ⁿ jít k nule či k nějakému kladnému číslu. Víme, že 1^∞ může být cokoliv, protože to je neurčitá mocnina, a bohužel pro nás, sin(n) může být libovolně blízko k 1 i pro velice velká čísla n. Není to nicméně nikdy přesně rovno 1. sin(n) je vždy o něco méně než jedna a umocňujeme to na ohromná čísla. Teď si připomeňme, že ty neurčité výrazy jsou vždy o rovnováze částí. Výraz 1^∞ může dát nulu za předpokladu, že posloupnost v bázi jde k 1 pomaleji (v určitém smyslu) než posloupnost v exponentu jde do nekonečna; zhruba řečeno, nekonečno musí být kvalitnější než 1 je jedničkou. Takže otázka teď je: Mohlo by být pravda, že pokaždé když se vezme n, pro které je |sin(n)| velice blízký k 1, pak je n už tak velké, že |sin(n)| umocněno na n je opravdu malé?

V našem případěm pokud je n vždy mnohem větší (bližší k nekonečnu) než je |sin(n)| k 1, pak daná posloupnost konverguje k nule. Jak o tom rozhodneme? To není možné s nástroji, které máme. Tento příklad vyžaduje velice důkladnou a obtížnou analýzu funkce sinus. Jak vidíte, odpověď na tuto limitu záleží na docela obskurních znalostech; naštěstí se takové věci nestávají často.

Zpět na Řešené příklady - Limita