Limita a srovnání

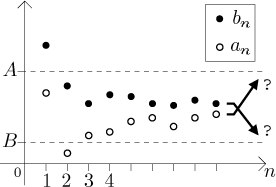
Zde se podíváme na vztah mezi konvergencí a srovnáním pomocí nerovnosti. Hlavním výsledkem je Věta o sevření.

 

Když máme dvě posloupnosti, existuje spojitost mezi jejich porovnáním člen po členu a srovnáním jejich limit:

Věta.
Nechť {an} je posloupnost konvergující k A a nechť {bn} je posloupnost konvergující k B.
(i)    Jestliže existuje přirozené číslo K takové, že an ≤ bn pro všechna n > K, pak také A ≤ B.
(ii)    Jestliže A < B, pak existuje přirozené číslo K takové, že an < bn pro všechna n > K.

Obě tvrzení by měla znít samozřejmě, když si nakreslíte pár obrázků. Pro uvěření prvnímu tvrzení si zkuste představit opak: že an ≤ bn, ale přesto A > B. Pokud se pokusíte takovou situaci nakreslit, rychle zjistíte, že to není možné. Toto samozřejmě není důkaz, ale napoví to.

Podobně pro druhé tvrzení si zkuste nakreslit situaci, kdy A < B, přesto členy an nepřestávají čas od času vyskakovat k či nad bn.

Poznámka: Není možné tvrdit "ostrou" verzi části (i). Přesně řečeno, i kdyby byly členy jedné posloupnosti vždy ostře větší než členy druhé, například pokud by platilo an < bn, nebylo by možné tvrdit, že následně A < B, protože dvě zcela různé posloupnosti mohou konvergovat k témuž číslu. Například (1/3)n < (1/2)n pro všechna přirozená čísla n, přesto obě konvergují k nule (viz geometrická posloupnost v části Teorie - Limita - Důležité příklady). Ta neostrá nerovnost ve větě je tedy to nejlepší, co se dá říct.

Podobně není možné mít tvrzení druhé části bez ostrých nerovností. Pokud bychom začali s předpokladem A ≤ B namísto A < B, tak bychom připustili případ A = B, v kterémžto případě mohou být členy těchto dvou posloupností v libovolném vzájemném vztahu, cokoliv je možné.

Všimněte si také, že jsme mohli formulovat tuto větu obecněji: Mohli jsme připustit, aby limity A či B byly nekonečné. Věta by pak pořád platila, ale nedala by nám informaci navíc. Pokud bychom například věděli, že an ≤ bn pro všechna n a že bn→∞, pak by věta poskytla závěr, že A ≤ ∞, což je ale ovšem pravda pro všechna čísla A a tudíž nic nového.

Dále si všimněte, že jsme ve větě předpokládali již od samého začátku, že obě posloupnosti konvergují. To bylo nutné, není totiž možné získat nějaký závěr ohledně konvergence jen na základě srovnání. Pokud bychom například věděli, že jedna posloupnost konverguje k 5 a druhá je u každého členu větší, nemohli bychom udělat žádný závěr o její konvergenci, protože má prostě příliš mnoho svobody (věta nám pouze říká, že kdyby tato druhá posloupnost byla konvergentní, tak její limita musí být přinejmenším 5). Abychom získali ze srovnání konvergenci, potřebujeme toho vědět více, viz Věta o sevření níže.

Někdy lze ale vynutit existenci nevlastní limity jen z jednostranného srovnání:

Věta.
Předpokládejme, že existuje přirozené číslo K takové, že an ≤ bn pro všechna n > K.
Jestliže an→∞, pak také bn→∞.
Jestliže bn→−∞, pak také an→−∞.

Tento obrázek by vás měl přesvědčit, že první tvrzení by mělo platit; to druhé je stejně zřejmé.

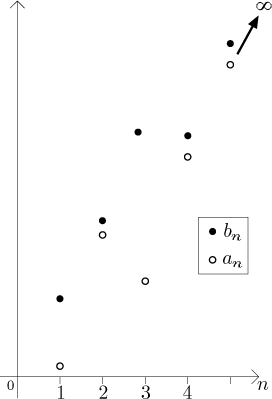
Všimněte si, že pokud máme srovnání a jedna z posloupností jde do nekonečna, pak lze tuto situaci využít k získání závěru jen v "polovině případů", pokud jde srovnání správným směrem. Jak je to myšleno? Uvažujme například situaci, kdy platí pro všechna n srovnání an ≤ bn. Pokud navíc víme, že an→∞, pak podle této věty rovněž bn→∞. Pokud bychom ale místo toho věděli, že bn→∞, pak nelze dojít k žádnému závěru ohledně an. Tato posloupnost je omezena jen shora do nekonečna jdoucí posloupností, takže jí zůstává příliš volnosti a může jít kamkoliv, třeba ani nemít limitu.

Věta o sevření

Poznamenali jsme, že jeden odhad ještě nestačí k vynucení konvergence. Na rozdíl od nevlastní limity, pokud chceme donutit členy nějaké posloupnosti, aby konvergovaly k určitému číslu, potřebujeme dvě omezení, abychom je tlačili z obou stran a zabránili posloupnosti utéct nahoru či dolů.

Věta (Věta o sevření).
Uvažujme tři posloupnosti {an}, {bn} a {cn}, splňující pro všechna n následující nerovnosti:

an ≤ bn ≤ cn.

Jestliže {an} konverguje k nějakému L a {cn} konverguje k témuž L, pak nutně také {bn} konverguje k tomuto L.

Proč by tohle mělo fungovat? To by mělo být jasné z následujícího obrázku:

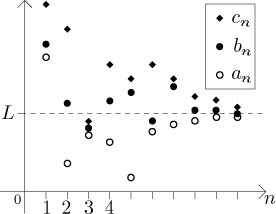
Větě se také říká "Věta o dvou strážnících".

Dodejme, že "pro všechna n" vlastně značí "pro všechna n použitá při indexaci posloupností". A protože konvergence se ve skutečnosti rozhoduje až na koncích posloupností, ne jejich začátcích, stačí dokonce předpokládat, že tyto nerovnosti jsou splněny pro "n dostatečně velká", neboli že existuje K takové, že nerovnosti platí pro všechna n > K.

Jako aplikaci si dokážeme následující výsledek.

Fakt.

Důkaz: Začneme následujícím pozorováním. Pro všechna celá čísla n máme

−1 ≤ (−1)n ≤ 1.

Když tyto nerovnosti vydělíme přirozeným číslem n, dostaneme

−1/n ≤ (−1)n/n ≤ 1/n.

Máme tedy danou posloupnost sevřenu z obou stran, neboli máme pro ni horní a dolní odhad. V jazyce Věty o sevření bychom si označili

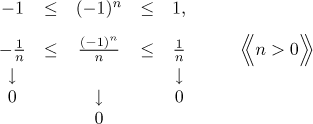
Protože −1/n→0 a 1/n→0, podle Věty o sevření také daná posloupnost konverguje k nule, přesně jak jsme tvrdili. Důkaz je hotov. Celou proceduru lze zapsat následovně (uděláme poznámku ohledně toho, že n je kladné, abychom vysvětlili, proč není nutné obrátit směr nerovností při dělení n).

Tento příklad byl typický. Výrazy, které oscilují, často způsobují potíže a obvyklé metody výpočtu limit pro ně selhávají, ale většina oscilujících výrazů má nějaké přirozené meze, což přímo volá po použití sevření.

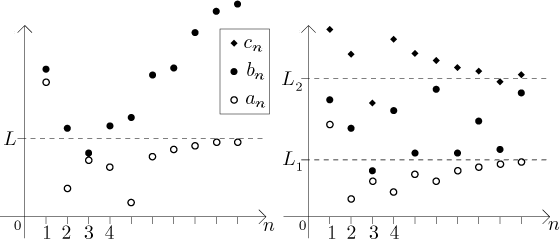
Poznámka: Správné sevření má dvě části. Nejprve se musí prozkoumat daná posloupnost kvůli nalezení horního a dolního odhadu. Za druhé, horní a dolní odhad musí konvergovat k témuž číslu. Kdybychom měli jen jeden odhad, nebo kdyby odhady nekonvergovaly k témuž číslu, nebylo by možné dojít k nějakému závěru. Ukazujeme to v následujících obrázcích, kde posloupnost {bn} může konvergovat k mnoha číslům či dokonce nekonvergovat vůbec. Vlevo máme pouze dolní odhad pro {bn}, která tak může utíkat vzhůru, jak se jí zachce; vpravo máme dva odhady, ale s různými limitami; {bn} zase zůstává příliš mnoho svobody.

Pro tipy ohledně správného používání sevření odkazujeme na Přehled metod, jmenovitě šuplík "srovnání a oscilace".

Někdy je efektivnější použít při sevření absolutní hodnotu, ale to funguje pouze pro posloupnosti konvergujících k nule:

Věta (Věta o sevření - verze s absolutní hodnotou).
Uvažujme posloupnosti {an} a {bn} splňující

|bn| ≤ an pro všechna n.

Jestliže {an} konverguje k 0, pak {bn} nutně také konverguje k 0.

V posledním příkladě jsme například také mohli postupovat následovně: Pro všechna n máme |(−1)n| ≤ 1. Následně také |(−1)n/n| ≤ 1/n pro všechna přirozená čísla n. Protože 1/n konverguje k nule, také daná posloupnost musí konvergovat k nule.

Věta o sevření má jeden pěkný důsledek, který je velmi užitečný při výpočtu limit.

Důsledek.
Když se omezená posloupnost vynásobí posloupností konvergující k nule, vznikne posloupnost konvergující k nule.
Když se omezená posloupnost vynásobí posloupností jdoucí do nekonečna, vznikne posloupnost konvergující k nule.

Krátce, "omezená krát nula je nula" a "omezená dělená nekonečnem je nula". To se často používá.

Posloupnosti a funkce
Zpět na Teorie - Limita