Metoda bisekce a Newtonova metoda

Uvažujme následující problém. Máme funkci f a chceme najít bod, ve kterém je hodnota f rovna dané hodnotě. Ukážeme dvě metody. Metoda bisekce je obecnější, hledá body, které splňují určitou vlastnost (a ta nemusí být nutně vázána na nějakou funkci, ale s funkcí je to ta nejpřirozenější situace). Na druhou stranu Newtonova metoda funguje jen na speciální případ "problému hodnoty", jmenovitě hledá bod, kde je daná funkce nulová.

Metoda bisekce

Tato metoda se používá v mnoha situacích k nalezení čísla s určitou vlastností. Používá vlastně dvě posloupnosti, ne jen jednu, a hned uvidíme proč. Hlavní idea bisekce je následující: Nějak najdeme (třeba uhádnutím) dvě čísla x_n < y_n taková, že hledané číslo leží mezi nimi. Pak se podíváme na jejich střed m_n = (x_n + y_n)/2. Pokud je tento střed hledané číslo, skončili jsme. Pokud ne, tak protože to číslo leželo v intervalu (x_n, y_n), musí nutně ležet v jednom z menších intervalů vzniklých jeho rozpůlením, neboli musí nutně ležet buď mezi x_n a m_n, nebo mezi m_n a y_n. Ať už je to jakkoliv, vezmeme příslušný pár jako nový počáteční pár s indexem n +1. Obrázek ukazuje dva kroky typického hledání jistého čísla x.

Protože se v každém kroku členy vzniklých dvou posloupností přiblíží na polovinu předchozí vzdálenosti, tak nakonec vymezí hledané číslo s libovolnou přesností.

Teď tuto myšlenku aplikujeme na hledání druhé odmocniny daného kladného čísla A.
Začneme tím, že uhádneme dvě kladná čísla x₀ < y₀ tak, aby x₀² < A < y₀². To znamená, že hledaná odmocnina musí ležet mezi nimi.
Teď definujeme obecný rekurzivní krok. Je-li dán pár x_n < y_n splňující x_n² < A < y_n², nalezneme střed m_n = (x_n + y_n)/2. Pokud máme štěstí, dostali jsme druhou odmocninu. Pokud ne, pak odmocnina musí ležet buď mezi x_n a m_n (jestliže x_n² < A < m_n²), nebo musí být mezi m_n a y_n. Ať už je to jakkoliv, prohlásíme dvě příslušná čísla za nový pár x_n+1 a y_n+1 a proces pokračuje. Jako příklad ukážeme, jak se najde druhá odmocnina z 19.3.

V další části ukážeme, jak se metoda bisekce používá k hledání kořenů funkcí. Metoda bisekce je obecně dost pomalá při získávání nutné přesnosti (v každém kroku se možná chyba pouze zmenší na polovinu), ale je značně spolehlivá; stačí jen najít nějaké vymezení hledaného čísla k nastartování procedury a metoda funguje. Všimněte si, že metoda pro nalezení druhé odmocniny vysvětlená níže zmenšuje chybu mnohem rychleji.

Poslední poznámka se týká volby středu. Jsou modifikace bisekčního algoritmu, které fungují rychleji díky tomu, že se nevolí střed, ale nějaký bod, od kterého se čeká lepší fungování. Jsou-li dány x_n a y_n, tak v určitém kroku testujeme, jak se blíží ke splnění dané podmínky, v našem příkladě jak se jejich druhá mocnina blíží k A. Je přirozené očekávat, že pokud by bylo řekněme y_n² mnohem blíž k A než x_n², pak skutečná druhá odmocnina z A bude blíž k y_n než k x_n. Takže místo zkoušení středu m_n bychom v dalším kroku zkoušeli číslo poněkud blíže k y_n. Přesná volba se obvykle dělá proporčně, podle toho, jak relativně blízko jsou y_n a x_n k hledané vlastnosti.

Jednou z častých otázek v analýze je hledání kořene dané funkce. Přesně řečeno, je dán vzorec pro f (x) a my chceme najít číslo r splňující f (r) = 0 (pokud vůbec existuje). Pro kvadratické polynomy je to snadné pomocí známého vzorce, ale příslušné vzorce pro kořeny kubických polynomů jsou dost hnusné a pro polynomy stupně 4 a víc už ani vzorce nejsou. Jiné funkce než polynomy jsou ještě horší. Dokážete například najít číslo x splňující e^x + x = 0? To je mimochodem pro matematiku typické, otázky, které se dají velmi jednoduše položit, se často ukážou velmi obtížné.

Jedna možnost je aplikovat již probranou metodu bisekce. Fungovalo by to následovně:

Předpokládejme, že máme funkci f (x), chceme najít číslo r splňující f (r) = 0. Předpokládejme dále, že máme čísla x₀ < y₀ taková, že hodnoty f (x₀) a f (y₀) mají rozdílná znaménka (kdyby jedno z nich bylo nula, pak jsme už našli kořen a procedura skončila). Pak se zdá rozumné předpokládat, že hledaný kořen leží mezi nimi, pro spojité funkce to určitě platí (viz Věta o mezihodnotě v sekci Funkce - Teorie - Reálné funkce - Spojitost).

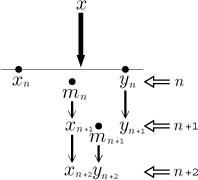
Definujeme posloupnosti {x_n} a {y_n} takto:

Jsou-li dány x_n a y_n takové, že f (x_n) a f (y_n) mají rozdílné znaménko, uvažujme jejich střed m_n = (x_n + y_n)/2.

Jestliže f (m_n) = 0, našli jsme kořen a procedura skončila.
Jestliže f (x_n) a f (m_n) mají rozdílná znaménka, definujeme x_n+1 = x_n a y_n+1 = m_n.
Jestliže f (m_n) a f (y_n) mají rozdílná znaménka, definujeme x_n+1 = m_n a y_n+1 = y_n.

Všimněte si, že jestliže má f rozdílné znaménko v x_n a y_n a jestliže f (m_n) není nula, pak se jedna z výše uvedených alternativ musí stát, jeden z nových párů musí mít rozdílná znaménka v f, kořen je pak mezi nimi (snad).

Jak už jsme poznamenali, tato metoda je spolehlivá, ale pomalá. Jedním z nejpopulárnějších nástrojů k hledání kořene je Newtonova metoda. Předokládá, že daná funkce má derivaci.

Newtonova metoda.
Vybereme nějakou počáteční hodnotu x₀. Pak definujeme rekurzivně
(1) x_n+1 = x_n − f (x_n)/f ′(x_n), n = 0,1,2,3,...

Jestliže tato posloupnost konverguje, pak její limita r splňuje f (r) = 0.

Jak jsme dostali vzorec pro Newtonovu metodu? Je to vlastně docela snadné pomocí elementární geometrie, pokud vás to zajímá, klikněte sem. Najdete tam také jednoduchý příklad, u kterého tato metoda selže, což se může snadno stát. To je hlavní nevýhoda Newtonovy metody. Na druhou stranu, pokud funguje, pak velice rychle dosáhne žádané přesnosti. V další části ukážeme jednu užitečnou aplikaci.

Máte kladné reálné číslo A. Jak najdete jeho druhou odmocninu? Pokud zrovna nemáte ohromné štěstí, tak odpovědí asi nebude celé číslo. Součástí otázky je tedy další důležitá informace: Jak přesně se chce odpověď.

Poznamenejme, že v matematice lze odpovědět zcela přesně. Nakreslí se srandovní šibenice nad A a řekne se: Tady je ta odmocnina. A to je také správná odpověď. Nicméně v reálném světě (a v matematice, když se začne aplikovat) je potřeba znát odpověď v desetinném tvaru. Účel, pro který tuto odmocninu hledáme, také rozhodne, jaká je žádaná přesnost. Pokud si tu odmocninu chcete zaznačit na reálné ose, nemá smysl žádat o víc než dvě desetinná místa, hrot vaší tužky je stejně tlustší. Na druhou stranu je možné, že chcete tuto odmocninu použít ve složitějším výpočtu (například v inženýrství), kde je třeba pěti desetinných míst. Možná jste dokonce výrobce kalkulaček, pak potřebujete znát odpověď na řekněme 13 míst.

Takže zpátky k otázce: jak najdeme druhou odmocninu z A? Existuje algoritmus pro "tužku a papír" k hledání odmocnin, který jste se asi naučili na střední škole (a zase už zapomněli), ten ale není zrovna nejvhodnější pro počítače. Zkusíme na to použít Newtonovu metodu, a to trikem: budeme hledat kořen funkce f (x) = A − x². Vidíme, že druhá odmocnina A je kladným kořenem funkce f. Co se stane, pokud aplikujeme Newtonovu metodu v této situaci? Dostaneme zajímavou posloupnost.

Definujeme rekurzivně
(0)    a₀ = A (nebo jiná hodnota, vlastně na ní moc nezáleží),
(1)    a_n+1 = 1/2(a_n + A/a_n), n = 0,1,2,3,...

Dá se dokázat, že tato posloupnost konverguje a její limita je přesně druhá odmocnina z A (podobné posloupnosti jsou i pro další odmocniny). Tento algoritmus se snadno naprogramuje do počítače a najde odmocninu dost rychle.

Například moje kalkulačka říká, že odmocnina ze dvou je asi 1.4142136. Zkusíme naši posloupnost:
a₀ = 2, a₁ = 1.5, a₂ = 1.4166667, a₃ = 1.4142157, a₄ = 1.4142136.
Jak vidíte, funguje to docela dobře. Dá se dokázat, že každá iterace této procedury zhruba zdvojnásobí počet desetinných míst, kteé jsou správně.

Zpět na Teorie - Aplikace