Spojitost reálných funkcí

Nejprve představíme spojitost v bodě, pak prozkoumáme její vlastnosti a nespojitosti. Další dvě části se zabývají spojitostí na množině a vlastnostmi spojitých funkcí na intervalu.

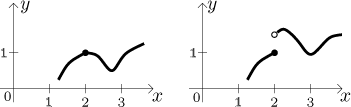
V Příkladě, kterým jsme uvedli funkce, jsme v jednu chvíli použili toho, že auto projíždí všechna mezilehlá místa, nemůže okamžitě skákat z jednoho místa na jiné. Tomu se říká spojitost. Když se podíváte na následující dva grafy, měli byste vidět jeden základní rozdíl. Zatímco ten první lze nakreslit bez zvednutí tužky z papíru, u druhého musíme udělat skok.

Tento rozdíl může mít dalekosáhlé důsledky. Teď potřebujeme nějak vyjádřit pocit "spojenosti" formálně; bohužel, jsou mnohem horší funkce než ta napravo výše, takže budeme muset začít techničtěji a začneme zkoumáním situace v daném bodě. Aby byla funkce spojitá v daném bodě a, zhruba řečeno je třeba následující. Funkce musí být v daném bodě definovaná, abychom měli v grafu f tečku reprezentující hodnotu f (a). Když kreslíme graf f a tužka se pohybuje tak, že odpovídající x-ová souřadnice prochází a, pak graf, který kreslíme, musí jít skrz bod (a, f (a)). To se mnohem lépe vidí, když si představujeme, jak se x blíží zleva a zprava k a, pak chceme, aby odpovídající části grafu šly k (a, f (a)).

Uvažujme příklad nahoře a bod a = 2. V obou případech má funkce hodnotu 1 = f (2), takže kritický bod grafu je (2,1). Pokud začneme kreslit graf na levém obrázku a začneme se přibližovat k bodu (2,1), pak ať už jdeme zleva či zprava, křivka vždy dojde do bodu (2,1). V druhém případě vše funguje, když se přibližujeme k bodu (2,1) zleva, ale když začneme jít k bodu (2,1) zprava, tak graf nejde do bodu (2,1), ale do nějakého jiného bodu, což je chování, které nesouhlasí s tím, co cítíme pod spojitostí v bodě 2.

Proto vlastně porovnáváme dvě věci, hodnotu f přímo v a a chování f okolo a, ale pro to už máme jméno, říkáme tomu limita. Pro nepřerušený graf v a potřebujeme, aby se tyto dva rozdílné typy informace (v bodě, okolo onoho bodu) shodovaly.

Definice.
Nechť f je funkce definovaná na nějakém okolí bodu a. Řekneme, že funkce f je spojitá v a, jestliže limita f v a konverguje k f (a).

Než se pustíme do dalšího zkoumání spojitosti, poznamenejmě, že když jsme se blížili k danému bodu, měli jsme na vybranou, jestli se blížíme zleva nebo zprava. Pro spojitost jsme museli uvažovat oba způsoby. Jsou nicméně situace, kdy nás zajímá jen jedna strana. To může mít rozumný důvod, například si všimněte, že když v tom druhém příkladě nahoře ignorujeme část doprava od bodu 2, tak je graf najednou "lepší", beze skoků.

Definice jednostranné spojitosti je skoro stejná jako ta výše, jen musíme omezit x na příslušnou stranu od a.

Matematicky vyjádříme spojitost a jednostranné spojitosti následujícími rovnostmi:

Pokud použijeme krátkého značení pro jednostrannou limitu, pak se dá spojitost zleva a zprava vyjádřit takto:

f (a^-) = f (a),         f (a⁺) = f (a).

Poznamenejme, že někteří autoři definují spojitost jinak, ale nakonec to vede na stejný pojem. Přemýšlení o této druhé definici může být velmi užitečné pro ty, kteří se snaží o dobré pochopení analýzy, nabízíme ji zde.
Pro pokročilou technickou poznámku se můžete podívat sem.

Pokud máte nějakou představu o tom, co je to spojitost, pak by vás následující věta neměla překvapit.

Věta.
Funkce f je spojitá v nějakém bodě a tehdy a jen tehdy, jestliže je spojitá v a jak zleva tak zprava.

Začneme nespojitostmi.

Definice.
Nechť f je funkce definovaná na nějakém okolí bodu a. Řekneme, že a je bodem nespojitosti funkce f, jestliže f není spojitá v a.

Nespojitosti lze klasifikovat podle toho, jak moc se spojitost pokazí, tedy podle toho, jak moc selže rovnost

Je toho více, co se může pokazit, začneme od toho nejmenšího problému.

Klasifikace nespojitostí:

1. Odstranitelná nespojitost.
Řekneme, že funkce f má odstranitelnou nespojitost v bodě a, jestliže má vlastní limitu v a, ale tato limita není rovna f (a).

To je ten nejhezčí způsob, máme téměř vše, co je ke spojitosti třeba, jen malinko chybí. Typický případ:

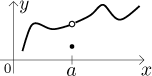
Teď vidíte, proč se to jmenuje odstranitelná nespojitost. Stačí změnit definici f v jediném bodě, jmenovitě v a, a nová funkce bude spojitá. Přesně, definujeme-li

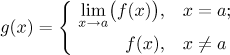
dostaneme funkci spojitou v a. Intuitivně prostě posuneme bod grafu tak, aby vyplnit díru.

2. Skoková nespojitost.
Řekneme, že funkce f má skokovou nespojitost v bodě a, jestliže má obě vlastní jednostranné limit v a, ale ty si nejsou rovny.

Když se jednostranné limity nerovnají, pak limita jako taková neexistuje. Tento případ je tedy o něco horší než odstranitelná nespojitost, ale existence jednostranných limit z toho ještě pořád dělá pěkný případ. Zde jsou dva typické příklady skoků, ten nalevo je alespoň spojitý v a zprava:

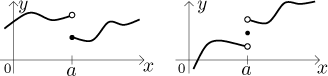
Teď zase vidíte, proč se to tak jmenuje. Pokud bychom nyní chtěli nespojitost spravit, nestačila by změna v jednom bodě. Abychom "napojili" funkci v a, museli bychom posunout půlku funkce nahoru či dolů.

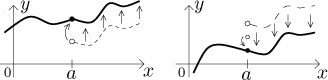
Není to tedy tak pěkné jako odstranitelná nespojitost, ale pořád se z toho dá vyrazit spojitá funkce.

3. Podstatná nespojitost.
Řekneme, že funkce f má podstatnou nespojitost v bodě a, jestliže nemá jednu či obě vlastní jednostranné limity v a.

Zde jsme naházeli všechny ostatní případy. Mají jedno společné, funkci nejde upravit tak, aby byla spojitá v a, pouhým posunutím části grafu. Některé typické příklady jsou zde:

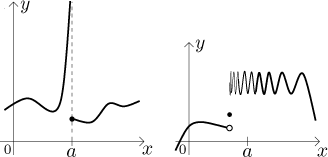
Na prvním obrázku máme jednostranné limity, ale jedna z nich není vlastní. Evidentně nelze posunou pravou půlku tak, aby se graf napojil. Ale i tak je to pořád ještě docela dobrý případ, protože vidíme určité tendence a máme užitečnou informaci. Vrátíme se k takovýmto příkladům, až budeme hovořit o asymptotách.

Na druhém obrázku limita zprava neexistuje, dokonce ani nevlastní, takže je to horší situace.

Poznámka: Jako obvykle přichází varování o terminologii. Někteří autoři rozlišují nespojitosti prvního, druhého a třetího druhu (prvního je odstranitelná, druhého skoková, třetího podstatná).

Spojitost a operace.

Příklad.
Než se pustíme dále, asi bychom se měli vypořádat s některými nesprávnými představami. Ty obrázky výše byly příliš pěkné v jednom směru. Abychom je mohli dobře kreslit, udělali jsme je okolo bodu a pěkné. Spojitost v a nám ale dává jen informaci o tomto konkrétním bodě a určitých tendencích kolem, nic víc. Uvažujme například tuto funkci.

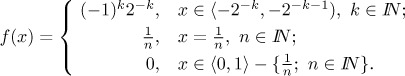
Jak to vypadá? Nejprve se podíváme na zápornou polovinu, interval ⟨−1,0). Na první polovině, na intervalu ⟨−1,−1/2), je funkce konstanta 1. Pak na intervalu ⟨−1/2,−1/4) je funkce rovna −1/2. Na intervalu ⟨−1/4,−1/8) je funkce rovna 1/4. Pokračujeme tímto způsobem, pokaždé vezmeme polovinu části, která ještě zbyla, a uděláme tam funkci konstantní, polovinu předchozí hodnoty a s opačným znaménkem.

Na intervalu ⟨0,1⟩ je funkce definována jinak. Začneme tím, že funkci položíme rovnu 0, ale pak v bodech tvaru 1/n nastavíme hodnotu na úroveň 1/n.

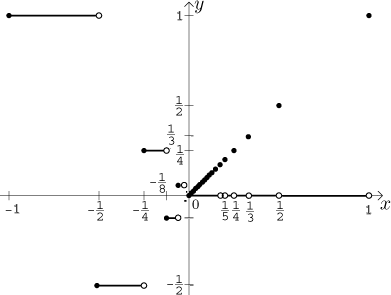
Protože pro každé x máme | f (x)| < 2|x|, vyplývá z toho (například díky Větě o sevření), že funkce má limitu v nule a ta je rovna 0. Máme také f (0) = 0. Proto je tato funkce spojitá v nule, na druhou stranu bychom asi neřekli, že je kolem 0 pěkná.

Pro další příklad podivné a přesto spojité funkce se podívejte na "Pilovité" funkce v části Teorie - Elementární funkce. Pokud vám ani to nestačilo, v sekci Dirichletova funkce je podivná funkce, která je spojitá v 0, ale nemá dokonce ve svém grafu žádné nepřerušované části.

Definice.
Nechť f je funkce, nechť M je podmnožina definičního oboru f. Řekneme, že funkce f je spojitá na M, jestliže je spojitá v každém bodě M když ji uvažujeme jako funkci na M.

Toto je pěkná definice, která se používá obecně, ale pro praktické použití s reálnými funkcemi není úplně nejlepší. Uděláme tedy speciální definici pro speciální typ množiny: interval.

Definice.
Nechť f je funkce definovaná na nedegenerovaném intervalu I. Řekneme, že funkce f je spojitá na intervalu I, jestliže je spojitá v každém vnitřním bodě I a rovněž v těch krajních bodech, které náleží do I, z odpovídající strany.

Uvažujme například funkci f definovanou na intervalu I = ⟨a,b). f je spojitá na I, jestliže je spojitá ve všech bodech z (a,b) a spojitá zprava v a. Zde je příklad takové funkce.

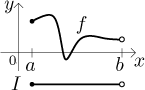
Tato definice platí i pro intervaly nekonečné, s nekonečnem jako jedním či oběma koncovými body. Když teď řekneme, že funkce je spojitá na množině, tak v případě, že ta množina je nedegenerovaný interval, použijete tuto novou definici. Jestliže je tato množina sjednocení nedegenerovaných intervalů, pak spojitost na této množině bude znamenat spojitost na každém z těchto intervalů dle této nové definice. Jedině pokud jde o nějakou jinou množinu, použijeme definici původní, ale s takovými množinami se setkáváme zřídka.

Zavedeme ještě jednu definici, abychom mohli rychle říct, že funkce je co se týče spojitosti nejlepší možná.

Definice.
Nechť f je funkce. Řekneme, že je spojitá, jestliže je spojitá na svém definičním oboru.

Teď se konečně dostáváme k tomu zajímavému. Ten příklad nahoře o funkci spojité v 0 ukázal, že znát spojitost v jednom konkrétním bodě nepomůže k tomu, aby funkce byla "pěkná", dokonce jsme ji ani neuměli pořádně nakreslit, měla příliš mnoho skoků okolo nuly zprava i zleva. Jakmile ale víme, že funkce je spojitá na intervalu, pak víme, že ji lze na něm nakreslit jako nepřerušovanou čáru. To pořád ještě nezaručuje, že funkce bude pěkná a půjde ji rozumně nakreslit (viz například "Pilovité" funkce v části Teorie - Elementární funkce), ale funkce spojité na intervalech jsou lepší než většina ostatních.

Věta (spojitost a operace).
Nechť f,g jsou funkce spojité na množině M. Pak jsou funkce f + g, f − g a f⋅g spojité na M. Funkce f /g je spojitá na množině M − {x; g(x) = 0}.

Nechť f je funkce spojitá na množině M, nechť g je funkce spojitá na množině f (M). Pak složená funkce f ○ g je spojitá na M.

Zmínili jsme se, že funkce jsou často zkoumány zvlášť na každém intervalu jejich definičních oborů a informace je pak dána dohromady. Jak to funguje u spojitosti? Uvažujme následující situaci: Máme funkci f a víme, že je spojitá na intervalu I a na intervalu J. Co můžeme říct o spojitosti na množině M = I ∪ J? Jsou tři případy:

• Pokud se tyto dva intervaly překrývají (tedy pokud jejich průnik není prázdný), pak mají alespoň jeden společný bod. Protože tento bod je společný obou kouskům grafu, pěkně je spojí, proto je funkce zase spojitá na sjednocení.

  

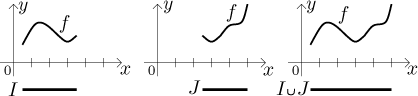
• Pokud jsou intervaly disjunktní a nejsou vedle sebe, pak je funkce také spojitá na jejich sjednocení M. Proč je tomu tak? Pokud intervaly nemají společné body, pak odpovídající (pěkně nepřerušované) kusy grafu nejsou vedle sebe, proto se nemůže nic pokazit, když se na ně podíváme jako na jeden celek. Podobný závěr dostaneme, když jsou intervaly vedle sebe, tj. když mají společný koncový bod, ale jsou tam oba otevřené. Tento bod pak nepatří ani jednomu z nich, není tedy částí jejich sjednocení a rozdělí odpovídající dva kusy grafu. Nemusíme se tam tedy starat o spojitost.

  

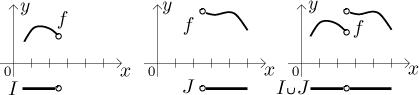
• Třetí případ je jediný "zajímavý", protože zde je nutno něco dělat. Jediný případ nepokrytý předchozími dvěma je, když se tyto dva intervaly dotýkají, tj. pokud mají společný koncový bod, řekněme c, a tento koncový bod náleží přesně do jednoho z těchto intervalů. Pak také náleží do sjednocení M, a protože je to bod styku obou intervalů, náleží do vnitřku množiny M. Proto je graf f definován jak nalevo, tak napravo od c a musíme se zajímat o to, zda se odpovídající dva kusy spojují dobře či ne. Musíme se tedy podívat na jednostranné limity v c. Pokud se shodují, pak se kusy grafu dobře spojují a máme spojitost na M, v opačném případě bude nějaká nespojitost v c (nemusí to být zrovna skoková, protože funkce spojitá na otevřeném intervalu nemusí mít jednostranné limity v koncových bodech).

  

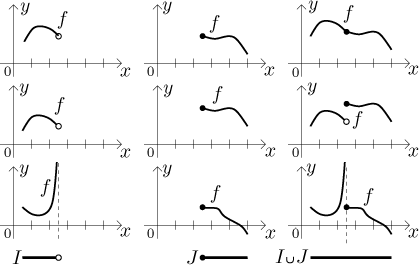
Tyto úvahy jsou užitečné zejména při zkoumání funkcí definovaných po částech, protože pak dáváme dohromady kousky funkce uvažované na rozličných množinách a ty množiny se v typickém případě setkávají přesně tak, jak jsme to probírali ve třetí alternativě.

Při práci s funkcí nám někdy vadí, když je někde nulová. Jako příklad uvažujme podíl 1/ f. Aby existoval, potřebujeme vědět, že je f nenulová, a to pokud možno na nějaké větší množině. Někdy to ale nestačí. Podmínka, že f není na určité množině nula, totiž nezakazuje, aby se na této množině f nepřibližovala libovolně blízko k 0, což je něco, co by se nám nemuselo líbit (například by to znamenalo, že podíl 1/ f na té množině není omezený).

Často proto požadujeme více, chceme, aby f byla oddělena (separována) od nuly. To znamená, že okolo 0 existuje určitý pruh, do kterého f nevstoupí. Vyjádřeno pomocí nerovnosti to znamená, že existuje určitá konstanta k > 0 taková, že | f | > k na uvažované množině. To může být velmi užitečné, například podíl 1/ f je pak na té množině omezený. Alternativní zápis separace f od nuly na M je inf_M( f ) > 0.

Spojitost nabízí šanci, jak dostat takovou separaci alespoň lokálně.

Věta.
Předpokládejme, že funkce f splňuje f (a) ≠ 0. Jestliže je f spojitá v a, pak existuje okolí U bodu a a konstanta k > 0 taková, že | f | > k na U.

Poznamenejme, že bez spojitosti závěr nemusí platit. Bez spojitosti dokonce nemáme ani slabší tvrzení, že f ≠ 0 na U.

Teď přejdeme na vlastnosti funkcí spojitých na intervalu. Začneme definicí:

Definice.
Řekneme, že funkce f splňuje vlastnost mezihodnoty (nebo Darbouxovu vlastnost) na množině M, jestliže pro libovolné dva body x,y z M a libovolnou hodnotu d mezi čísly f (x), f ( y) existuje číslo c v M splňující f (c) = d.

Krátce, pro libovolné dvě hodnoty, kterých funkce s vlastností mezihodnoty nabývá, musí nabývat i všechny hodnoty mezi nimi. Obrázek naznačí význam této definice.

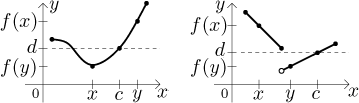
První situace je typická, tj. "pěkná". Druhý příklad také splňuje vlastnost mezihodnoty, ale dělá to poněkud nečekaným způsobem. Bod c, který jsme našli pro vyznačené d, neleží mezi x a y! To je naprosto v pořádku, definice nevyžadovala nějaké speciální umístění c, jen jeho existenci. Zkuste si u druhého příkladu jiné volby x,y a jiné hodnoty d, abyste se ujistili, že opravdu splňuje vlastnost mezihodnoty. Nicméně malá změna ve funkci už to pokazí:

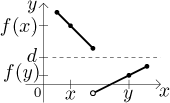
Zkuste si představit další funkce, které nesplňují vlastnost mezihodnoty. Když to děláte, měli byste začít mít pocit, že selhání vlastnosti mezihodnoty má něco společného s tím, že funkce má skoky. Jak jsme viděli, ne každá funkce se skoky selže ohledně této vlastnosti, ale pokud víme, že nějaká funkce skoky nemá, pak to už zaručuje vlastnost mezihodnoty za předpokladu, že množina M je interval (včetně nekonečného).

Pro další výsledek o vlastnosti mezihodnoty viz derivace jako funkce v části Derivace - Teorie - Úvod - Derivace a základní vlastnosti.

Důsledek.
Nechť f je funkce spojitá na intervalu ⟨a,b⟩. Jestliže mají hodnoty f (a), f (b) rozdílná znaménka, pak existuje nějaký kořen funkce f v intervalu (a,b).

Toto tvrzení je teoretickým základem populární metody bisekce k nalezení kořene, viz Metoda bisekce v části Posloupnosti - Teorie - Aplikace. Pomáhá také v situacích, kdy chceme určit znaménko nějaké funkce. Důsledek říká, že aby se spojitá funkce změnila z kladné na zápornou či naopak, musí při tom překročit osu x. To se dá reformulovat takto: Pokud taková funkce někde nemá kořen, pak tam nemůže měnit své znaménko.

Důsledek.
Nechť f je funkce spojitá na intervalu I. Nechť a,b jsou dva sousední nulové body f z tohoto intervalu, tj. mezi body a a b nejsou žádné další nulové body f. Pak je buď f vždy kladná na (a,b) nebo je f vždy záporná na (a,b).

Toto je základem další populární metody. Když zkoumáme znaménko nějakého výrazu, často začneme tím, že najdeme jeho nulové body. Tyto se stanou dělícími body, kde se znaménko může měnit, a rozdělí reálnou osu na intervaly, na kterých je znaménko neměnné. Pro určitý interval se pak příslušné znaménko určí tak, že se jednoduše do daného výrazu dosadí nějaký bod.

V předchozí sekci jsme definovali supremum, infimimum, minimum a maximum a poznamenali jsme, že minimum a maximum nemusí existovat dokonce ani pro omezené funkce na omezeném intervalu. Máme nicméně následující fakt.

Věta (o extrémní hodnotě).
Každá funkce spojitá na omezeném uzavřeném intervalu nabývá své maximum a minimum na tomto intervalu.

To také znamená, že spojitá funkce na omezeném uzavřeném intervalu musí být omezená.

Tyto dvě věty dají dohromady následující tvrzení:

Jestliže f je spojitá funkce na omezeném uzavřeném intervalu I, pak zobrazuje I na nějaký omezený uzavřený interval.

Víme, že ryze monotonní funkce na intervalu musí být prostá, proto tam má inverzní funkci. Pokud je funkce také spojitá, tato implikace se stane ekvivalencí; inverzní funkce jak navíc také pěkná.

Věta.
Nechť f je funkce spojitá na intervalu I. Pak f je prostá na I tehdy a jen tehdy, jestliže je ryze monotonní na I. Pokud tomu tak je, pak příslušná inverzní funkce k f je také spojitá na svém definičním oboru.

Monotonie reálných funkcí
Zpět na Teorie - Reálné funkce