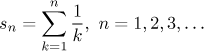
Zde se podíváme na harmonickou řadu. Abychom vyšetřili její konvergenci, případně našli její součet, potřebujeme prozkoumat posloupnost jejích částečných součtů:
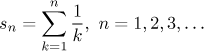
Tuto posloupnost je také možné definovat rekurzivně:
(1) s1 = 1,
(2) sn = sn−1 + 1/n,
pro n = 2,3,4,...
Protože každý další člen se získá přičtením kladného čísla k předchozímu, tato posloupnost je rostoucí. Jsou tedy dvě možnosti. Buď je tato posloupnost omezená a konverguje, nebo není omezená shora a jde do nekonečna. Co je správná odpověď?
Je snadné napsat jednoduchý program pro počítač či programovatelnou kalkulačku, který nám spočítá n-tý člen této posloupnosti. Pak dostaneme například toto:
s100 = 5.18738,
s1000 = 7.48548,
s10000 = 9.78761.
Co se stane, když zkusíme trik s následnými členy? Například
s1000000 = 14.35736 (šest nul v indexu) a
s1001000 = 14.35831. Čověk by si tipnul, že tato posloupnost
konverguje a limita je nejspíš zhruba 14.36. Není ovšem těžké ukázat, že ve
skutečnosti
Pokud máte pocit, že tento příklad je příliš jednoduchý a prokoukli byste
jej, vytáhněte kalkulačku a zkuste dosadit pár čísel do